题目内容
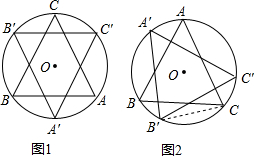 如图,边长为2的等边三角形ABC内接于⊙O,将△ABC绕圆心O沿顺时针方向旋转得到△A′B′C′,A′C′分别与AB、AC交于E、D两点,设旋转角为α(0°<α<360°).
如图,边长为2的等边三角形ABC内接于⊙O,将△ABC绕圆心O沿顺时针方向旋转得到△A′B′C′,A′C′分别与AB、AC交于E、D两点,设旋转角为α(0°<α<360°).(1)当△A′B′C′与△ABC第一次完全重合时,α=
(2)当α=60°时,(如图1),则该图形
A.是中心对称图形,但不是轴对称图形
B.是轴对称图形,但不是中心对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,又不是中心对称图形
(3)如图2,当0°<α<120°时,△ADE的周长是否会发生变化?若会变化,请说明理由;若不会变化,请直接写出它的周长(不需要证明).
考点:圆的综合题
专题:
分析:(1)根据等边三角形的中心角为120°求解;
(2)当α=60°时,点A、A′、B、B′、C、C′为⊙O的6等份点,所有的三角形都是等边三角形,则可利用正六边形的性质得到所有该图形既是轴对称图形,又是中心对称图形;
(3)连接OC、OC′、OA、OA′、AA′、AC′,如图2,先根据旋转的性质得∠COC′=∠AOA′=α,AB=A′C′=2,根据圆心角、弧、弦的关系得到
=
,
则根据圆周角定理得∠A′C′A=∠CAC′,所有EC′=EA,再利用AB=A′C′得到
=
,则
=
,所有∠A′AB=∠AA′C′,则DA=DA′,于是得到
△ADE的周长=AD+DE+AE=DA′+DE+EC′=A′C′=2.
(2)当α=60°时,点A、A′、B、B′、C、C′为⊙O的6等份点,所有的三角形都是等边三角形,则可利用正六边形的性质得到所有该图形既是轴对称图形,又是中心对称图形;
(3)连接OC、OC′、OA、OA′、AA′、AC′,如图2,先根据旋转的性质得∠COC′=∠AOA′=α,AB=A′C′=2,根据圆心角、弧、弦的关系得到
 |
| AA′ |
 |
| CC′ |
则根据圆周角定理得∠A′C′A=∠CAC′,所有EC′=EA,再利用AB=A′C′得到
 |
| AB |
 |
| A′C′ |
 |
| BA′ |
 |
| AC′ |
△ADE的周长=AD+DE+AE=DA′+DE+EC′=A′C′=2.
解答:解: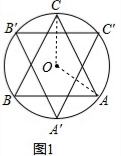 (1)连接OC、OA,如图1,
(1)连接OC、OA,如图1,
∵△ABC为等边三角形,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°,
∴当△A′B′C′与△ABC第一次完全重合时,α=120°;
故答案为120;
(2)当α=60°时,点A、A′、B、B′、C、C′为⊙O的6等份点,所有的三角形都是等边三角形,
所有该图形既是轴对称图形,又是中心对称图形.
故选C;
(3)△ADE的周长为2.
连接OC、OC′、OA、OA′、AA′、AC′,如图2,
 ∵等边三角形△ABC绕圆心O沿顺时针方向旋转α得到△A′B′C′,
∵等边三角形△ABC绕圆心O沿顺时针方向旋转α得到△A′B′C′,
∴∠COC′=∠AOA′=α,AB=A′C′=2,
∴
=
,
∴∠A′C′A=∠CAC′,
∴EC′=EA,
∵AB=A′C′,
∴
=
,
∴
-
=
-
,即
=
,
∴∠A′AB=∠AA′C′,
∴DA=DA′,
∴△ADE的周长=AD+DE+AE=DA′+DE+EC′=A′C′=2.
 (1)连接OC、OA,如图1,
(1)连接OC、OA,如图1,∵△ABC为等边三角形,
∴∠ABC=60°,
∴∠AOC=2∠ABC=120°,
∴当△A′B′C′与△ABC第一次完全重合时,α=120°;
故答案为120;
(2)当α=60°时,点A、A′、B、B′、C、C′为⊙O的6等份点,所有的三角形都是等边三角形,
所有该图形既是轴对称图形,又是中心对称图形.
故选C;
(3)△ADE的周长为2.
连接OC、OC′、OA、OA′、AA′、AC′,如图2,
 ∵等边三角形△ABC绕圆心O沿顺时针方向旋转α得到△A′B′C′,
∵等边三角形△ABC绕圆心O沿顺时针方向旋转α得到△A′B′C′,∴∠COC′=∠AOA′=α,AB=A′C′=2,
∴
 |
| AA′ |
 |
| CC′ |
∴∠A′C′A=∠CAC′,
∴EC′=EA,
∵AB=A′C′,
∴
 |
| AB |
 |
| A′C′ |
∴
 |
| AB |
 |
| AA′ |
 |
| A′C′ |
 |
| AA′ |
 |
| BA′ |
 |
| AC′ |
∴∠A′AB=∠AA′C′,
∴DA=DA′,
∴△ADE的周长=AD+DE+AE=DA′+DE+EC′=A′C′=2.
点评:本题考查了圆的综合题:熟练掌握圆心角、弧、弦的关系和圆周角定理定理、等边三角形的性质和旋转的性质;会运用等腰三角形的性质解决线段相等的问题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 一共要70元
一共要70元 一共要50元.
一共要50元.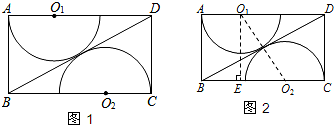 问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示).
问题:如图1,要在一个矩形木板ABCD上切割、拼接出一个圆形桌面,可在该木板上切割出半径相等的半圆形O1和半圆形O2,其中O1、O2分别是AD、BC上的点,半圆O1分别与AB、BD 相切,半圆O2分别与CD、BD相切.若AB=am,BC=bm,求最终拼接成的圆形桌面的半径(用含a、b的代数式表示).