题目内容
在出行中,主动采用能降低二氧化碳排放量的交通方式,谓之“低碳出行”.明明一家积极响应政府“绿色山城,低碳出行”的号召,今年2月-5月明明一家减少了驾车出行,他们将2月-5月驾车行驶的里程统计后绘制成以下两幅不完整的统计图:

(1)扇形统计图中x= ,并补全折线统计图;
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率.

(1)扇形统计图中x=
(2)某中学也积极参与“绿色山城,低碳出行”活动中,决定从4名广播社骨干成员中(其中两名男生,两名女生)选拔两名同学去演讲宣传,请用画树形图或列表的方法求所选出的两名同学恰好是一名男生一名女生的概率.
考点:折线统计图,扇形统计图,列表法与树状图法
专题:
分析:(1)先根据3月驾车行驶400千米,占40%,求出2月-5月驾车行驶的总里程数,再求出2月所占百分比,然后用1减去2、3、4月所占百分比,即可求出x的值;分别求出4、5两个月驾车行驶的里程数,即可补全折线统计图;
(2)列表得出所有等可能的情况数,找出刚好所选出的两名同学恰好是一名男生一名女生的情况数,即可求出所求的概率.
(2)列表得出所有等可能的情况数,找出刚好所选出的两名同学恰好是一名男生一名女生的情况数,即可求出所求的概率.
解答:解:(1)∵3月驾车行驶400千米,占40%,
∴2月-5月驾车行驶的总里程数为:400÷40%=1000,
∴2月所占百分比为300÷1000=30%,
∴5月所占百分比为1-30%-40%-20%=10%,
∴x=10;
4月驾车行驶的里程数为:1000×20%=200,
5月驾车行驶的里程数为:1000×10%=100.
折线统计图补充如下:

(2)设男生标记为A、B;女生标记为1、2,可能出现的所有结果列表如下:
共有12种可能的结果,且每种的可能性相同,其中刚好所选出的两名同学恰好是一名男生一名女生的结果有8种,
则P(一男一女)=
=
.
故答案为10.
∴2月-5月驾车行驶的总里程数为:400÷40%=1000,
∴2月所占百分比为300÷1000=30%,
∴5月所占百分比为1-30%-40%-20%=10%,
∴x=10;
4月驾车行驶的里程数为:1000×20%=200,
5月驾车行驶的里程数为:1000×10%=100.
折线统计图补充如下:

(2)设男生标记为A、B;女生标记为1、2,可能出现的所有结果列表如下:
| A | B | 1 | 2 | |
| A | / | (B,A) | (1,A) | (2,A) |
| B | (A,B) | / | (1,B) | (2,B) |
| 1 | (A,1) | (B,1) | / | (2,1) |
| 2 | (A,2) | (B,2) | (1,2) | / |
则P(一男一女)=
| 8 |
| 12 |
| 2 |
| 3 |
故答案为10.
点评:此题考查了扇形统计图,折线统计图,列表法与树状图法,概率公式,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.

练习册系列答案
相关题目
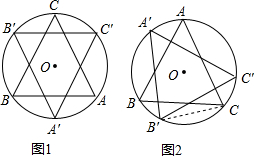 如图,边长为2的等边三角形ABC内接于⊙O,将△ABC绕圆心O沿顺时针方向旋转得到△A′B′C′,A′C′分别与AB、AC交于E、D两点,设旋转角为α(0°<α<360°).
如图,边长为2的等边三角形ABC内接于⊙O,将△ABC绕圆心O沿顺时针方向旋转得到△A′B′C′,A′C′分别与AB、AC交于E、D两点,设旋转角为α(0°<α<360°).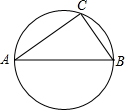 如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.
如图,⊙O的面积是25π,△ABC内接于⊙O,a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b),且a2+b2=c2.sinA、sinB分别是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两根.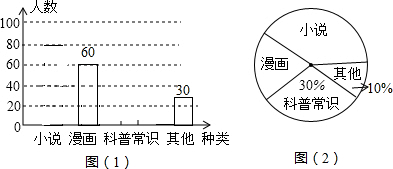
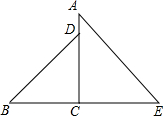 如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.
如图所示 AC⊥BE垂足为C,BD=AE,CD=CE,请探索直线BD与直线AE的位置关系.