题目内容
在Rt△ABC中，∠BAC=90°，AD⊥BC于D，AB=1，AC=2，则BD= ．
考点：勾股定理
专题：
分析：在Rt△ABC中，利用勾股定理求得BC的长度，然后利用射影定理来求BD的长度．
解答：
解：如图，∵在Rt△ABC中，∠BAC=90°，AB=1，AC=2，
∴由勾股定理，得
BC=
=
=
．
又AD⊥BC，
∴AB2=BD•BC，
则BD=
=
=
．
故答案是：
．
解：如图，∵在Rt△ABC中，∠BAC=90°，AB=1，AC=2，∴由勾股定理，得
BC=
| AC2+AB2 |
| 22+12 |
| 5 |
又AD⊥BC，
∴AB2=BD•BC，
则BD=
| AB2 |
| BC |
| 1 | ||
|
| ||
| 5 |
故答案是：
| ||
| 5 |
点评：本题考查了勾股定理．熟练掌握射影定理中几条线段的之间的关系是解题的关键．
练习册系列答案
相关题目
已知AB=AC，AD=AE，∠BAC=∠DAE=α，
如图，把矩形ABCD折叠，使点C与点A重合，折痕为EF，若AB=4，BC=8，求sin∠BAE的值．
已知，M是△ABC内的一点，MD⊥BC，ME⊥AC，MF⊥AB，且BD=BF，CD=CE，求证：AE=AF．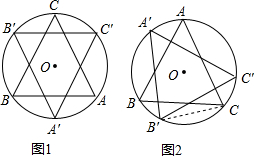
如图，边长为2的等边三角形ABC内接于⊙O，将△ABC绕圆心O沿顺时针方向旋转得到△A′B′C′，A′C′分别与AB、AC交于E、D两点，设旋转角为α（0°＜α＜360°）．
如图，把长方形纸片ABCD折叠，使A、C重合，EF为折痕，若AB=9，BC=3，求BF的长度．