题目内容
15.设α,β是一元二次方程x2-x-2=0的两个实数根,则α2-αβ+β2的值为7.分析 根据根与系数得关系得到α+β=1,αβ=-2,再变形原式得到(α+β)2-3αβ,然后利用整体代入的方法进行计算.
解答 解:∵α,β是一元二次方程x2-x-2=0的两个实数根,
∴α+β=1,α•β=-2,
∴α2-αβ+β2=(α+β)2-3αβ=12-3×(-2)=7.
故答案为:7.
点评 此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法,若方程ax2+bx+c=0两个根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.某购物中心一月份的营业额为100万元,三月份的营业额为121万元,设每月的平均增长率为x,则可列方程为( )
| A. | 121(1-x)2=100 | B. | 121(1+x)2=100 | C. | 100(1-x)2=121 | D. | 100(1+x)2=121 |
3.下列调查中,适合用普查方式的是( )
| A. | 了解某班学生“50米跑”的成绩 | |
| B. | 了解一批袋装食品是否含有防腐剂 | |
| C. | 了解江苏卫视“非诚勿扰”节目的收视率 | |
| D. | 了解一批灯泡的使用寿命 |
10.小林在某商店购买商品A,B共三次,第一、两次均按标价购物,第三次购物时,商品A,B同时打6折,三次购物商品A,B的数量和费用如下表:
(1)求出商品A,B的标价;
(2)求第三次购物时的总费用是多少?
| 购买商品A的数量(个) | 购买商品B的数量(个) | 购买总费用(元) | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 |
(2)求第三次购物时的总费用是多少?
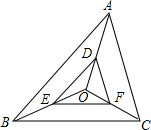 如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.
如图,O是△ABC内一点,D,E,F分别是OA,OB,OC上的点,DE∥AB,DF∥AC.