题目内容
某工厂生产的新产品按质量可分为6个档次,生产第一档次(即最低档次)的产品每件的利润为10元.已知该厂生产的产品每提高一个档次,每件产品的利润可增加2元.
(1)当工厂生产第四档次的产品时,每件的利润是多少元?
(2)如果工厂每天只安排生产同一档次产品,且每天能生产第一档次产品76件.由于生产工序不同,生产的产品每提高一个档次,一天的产量就减少4件,当工厂生产某一档次产品一天的总利润为1080元时,该厂这一天安排生产的是第几档次的产品?
(1)当工厂生产第四档次的产品时,每件的利润是多少元?
(2)如果工厂每天只安排生产同一档次产品,且每天能生产第一档次产品76件.由于生产工序不同,生产的产品每提高一个档次,一天的产量就减少4件,当工厂生产某一档次产品一天的总利润为1080元时,该厂这一天安排生产的是第几档次的产品?
考点:一元二次方程的应用
专题:
分析:(1)依题意可求出产品质量在第4档次的每件的利润.
(2)设生产产品的质量档次是在第x档次时,一天的利润是y,求出y与x的函数解析式,令y=1080,求出x的实际值.
(2)设生产产品的质量档次是在第x档次时,一天的利润是y,求出y与x的函数解析式,令y=1080,求出x的实际值.
解答:解:(1)10+2×(4-1)
=10+2×3
=10+6
=16(元)
答:每件的利润是16元.
(2)设生产产品的质量档次是在第x档次时,一天的利润是y,
由题意可得y=[10+2(x-1)][76-4(x-1)],
整理得y=-8x2+128x+640,
当利润是1080元时,即-8x2+128x+640=1080,
解得:x1=5,x2=11(11>6,不符合题意,舍去),
答:该厂这一天安排生产的是第5档次的产品.
=10+2×3
=10+6
=16(元)
答:每件的利润是16元.
(2)设生产产品的质量档次是在第x档次时,一天的利润是y,
由题意可得y=[10+2(x-1)][76-4(x-1)],
整理得y=-8x2+128x+640,
当利润是1080元时,即-8x2+128x+640=1080,
解得:x1=5,x2=11(11>6,不符合题意,舍去),
答:该厂这一天安排生产的是第5档次的产品.
点评:本题考查了一元二次方程的应用,难度一般,在市场营销问题中要根据题意先确定二次函数,再解一元二次方程,由一般到特殊.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
下列各组二次根式中,是同类二次根式的是( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列计算正确的是( )
| A、(a+2b)(a-2b)=a2-2b2 |
| B、(2x+3)2=4x2+9 |
| C、(a-4b)2=a2-8ab+4b2 |
| D、(-y-5)2=y2+10y+25 |
数轴上表示-2.2的点在( )
| A、-2与-1之间 |
| B、-3与-2之间 |
| C、2与3之间 |
| D、1与2之间 |
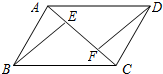 如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF,求证:△ABE≌△CDF.
如图,四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接ED,BF,求证:△ABE≌△CDF. 如图,点A、B、C、D在同一直线上,如果CE=BF,AB=CD且EC⊥AD,FB⊥AD,垂足为B、C.问AE∥DF吗?为什么?
如图,点A、B、C、D在同一直线上,如果CE=BF,AB=CD且EC⊥AD,FB⊥AD,垂足为B、C.问AE∥DF吗?为什么? 如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O.求证:∠ABD=∠ACE.
如图,在△ABC中,AB=AC,AD⊥BD,AE⊥CE,且AD=AE,BD和CE交于点O.求证:∠ABD=∠ACE.