题目内容
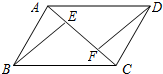如图，四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接ED，BF，求证：△ABE≌△CDF．考点：平行四边形的性质,全等三角形的判定
专题：证明题
分析：首先由平行四边形的性质可得AB=CD，AB∥CD，再根据平行线的性质可得∠BAE=∠DCF，∠BEC=∠DFA，即可根据AAS定理判定△ABE≌△CDF．
解答：证明：∵在平行四边形ABCD中AB=CD，AB∥CD，
∴∠BAC=∠DCA
又∵BE∥DF
∴∠BEF=∠DFE
∴∠BAE=∠CFD
∴在△ABE和△CDF中
，
△ABE≌△CDF．
∴∠BAC=∠DCA
又∵BE∥DF
∴∠BEF=∠DFE
∴∠BAE=∠CFD
∴在△ABE和△CDF中
|
△ABE≌△CDF．
点评：此题主要考查了平行四边形的性质，以及全等三角形的判定，关键是掌握①平行四边形的对边平行且相等；②全等三角形的判定方法：SSS、SAS、ASA、AAS、HL．
练习册系列答案
相关题目
| 2a |
| 6ab |
A、a
| ||
| B、12a2b | ||
C、a2
| ||
D、2a
|
下列式子中，符合代数式的书写格式的是（ ）
| A、a•20 | ||
| B、3÷a | ||
C、
| ||
D、2
|
如图，点O是直线AB上的一点，OM是∠AOC的平分线，ON是∠COB的平分线，求∠MOC和∠NOC有何关系？为什么？