题目内容
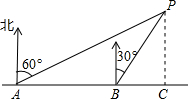 如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?(
如图,小明同学在东西方向的环海路A处,测得海中灯塔P在它的北偏东60°方向上,在A的正东400米的B处,测得海中灯塔P在它的北偏东30°方向上.问:灯塔P到环海路的距离PC约等于多少米?(| 3 |
考点:解直角三角形的应用-方向角问题
专题:
分析:根据等角对等边得出PB=AB=400米,再利用三角函数求出PC的长即可.
解答:解:如图,由题意,可得∠PAC=30°,∠PBC=60°,
∴∠APB=∠PBC-∠PAC=30°,
∴∠PAC=∠APB.
∴PB=AB=400米.
在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=400米,
∴PC=PB•sin∠PBC=400×
=200
=346.4≈346(米).
答:灯塔P到环海路的距离PC约等于346米.
∴∠APB=∠PBC-∠PAC=30°,
∴∠PAC=∠APB.
∴PB=AB=400米.
在Rt△PBC中,∠PCB=90°,∠PBC=60°,PB=400米,
∴PC=PB•sin∠PBC=400×
| ||
| 2 |
| 3 |
答:灯塔P到环海路的距离PC约等于346米.
点评:本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
下列式子中,互为同类项的是( )
| A、-xy2与y2x |
| B、18x2y2与9x2+y2 |
| C、a+b与a-b |
| D、-2a3b与3ab3 |
在平面直角坐标系中,点P的坐标为(4,0),以P为圆心,5为半径作⊙P,则直线y=kx+2(k≠0)与⊙P的位置关系是( )
| A、相交 | B、相离 |
| C、相切 | D、与k的取值有关 |
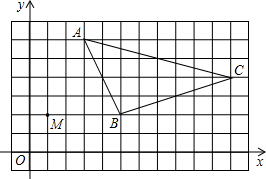 在如图所示网格图中,已知△ABC和点M(1,2)
在如图所示网格图中,已知△ABC和点M(1,2)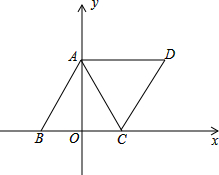 如图,在等边△ABC中,B(-1,0)、C(1,0),以底边BC的垂直平分线和BC所在直线建立平面直角坐标系,把△ABC绕着点C顺时针旋转60°的得到△DEF,(旋转后D与A、E与B、F与C对应)
如图,在等边△ABC中,B(-1,0)、C(1,0),以底边BC的垂直平分线和BC所在直线建立平面直角坐标系,把△ABC绕着点C顺时针旋转60°的得到△DEF,(旋转后D与A、E与B、F与C对应) 如图,在坡角为30°的斜坡上有两棵树,它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为
如图,在坡角为30°的斜坡上有两棵树,它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为