题目内容
在平面直角坐标系中，点P的坐标为（4，0），以P为圆心，5为半径作⊙P，则直线y=kx+2（k≠0）与⊙P的位置关系是（ ）
| A、相交 | B、相离 |
| C、相切 | D、与k的取值有关 |
考点：直线与圆的位置关系,一次函数的性质
专题：
分析：首先求出⊙P与y轴交点，进而得出直线y=kx+2与y轴交点，即可得出直线与圆的位置关系．
解答：解：∵点P的坐标为（4，0），以P为圆心，5为半径作⊙P，
∴AP=5，PO=4，
∴AO=3，
∵直线y=kx+2与y轴交于点（0，2），
∴无论k为何值，直线y=kx+2与⊙P的位置关系是相交．
故选：A．
∴AP=5，PO=4，
∴AO=3，
∵直线y=kx+2与y轴交于点（0，2），
∴无论k为何值，直线y=kx+2与⊙P的位置关系是相交．
故选：A．
点评：此题主要考查了勾股定理以及直线与圆的位置关系，根据已知得出直线y=kx+2与y轴交点是解题关键．
练习册系列答案
相关题目
下列整式中，（ ）是多项式．
| A、100t |
| B、v+2.5 |
| C、πr2 |
| D、0.1 |
用代数式表示“a的
与5的和”，结果是（ ）
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、a+
|
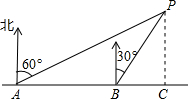如图，小明同学在东西方向的环海路A处，测得海中灯塔P在它的北偏东60°方向上，在A的正东400米的B处，测得海中灯塔P在它的北偏东30°方向上．问：灯塔P到环海路的距离PC约等于多少米？（
画出图中长方体的正投影．