��Ŀ����
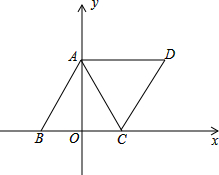 ��ͼ���ڵȱߡ�ABC�У�B��-1��0����C��1��0�����Եױ�BC�Ĵ�ֱƽ���ߺ�BC����ֱ�߽���ƽ��ֱ������ϵ���ѡ�ABC���ŵ�C˳ʱ����ת60��ĵõ���DEF������ת��D��A��E��B��F��C��Ӧ��
��ͼ���ڵȱߡ�ABC�У�B��-1��0����C��1��0�����Եױ�BC�Ĵ�ֱƽ���ߺ�BC����ֱ�߽���ƽ��ֱ������ϵ���ѡ�ABC���ŵ�C˳ʱ����ת60��ĵõ���DEF������ת��D��A��E��B��F��C��Ӧ����1������A��B��D����������߽���ʽ
���������ߵĶԳ����ϴ���һ�㣬ʹ���Ե�C��D��MΪ�������������ֱ�������Σ���ֱ��д����M�����ꣻ
��3����ֱ��BD�Ϸ������������Ƿ����һ��P��ʹ�á�PBD�����S��PBD=
| 1 |
| 4 |
���㣺���κ����ۺ���
ר�⣺ѹ����
��������1��������ת�����ʺ͵ȱ������ε��������AD��x�ᣬȻ��д����D�����꣬�����ô���ϵ��������κ�������ʽ���
��2�����ݶ��κ����ĶԳ��ԣ�AD��Գ��ᴹֱ�����Խ��㼴Ϊ����ĵ�M����DΪֱ�Ƕ���ʱ���������������ζ�Ӧ�߳ɱ������CM��Ȼ��д����M�����꼴�ɣ�
��3�����ô���ϵ������һ�κ�������ʽ���ֱ��BD�Ľ���ʽ�������P��y��ƽ�е�ֱ����ֱ��BD�ཻ�ڵ�Q����ʾ��PQ�������������ε������ʽ��ƽ���ı��ε������ʽ�г����̣����xֵ��Ȼ�����������߽���ʽ��⼴�ɣ�
��2�����ݶ��κ����ĶԳ��ԣ�AD��Գ��ᴹֱ�����Խ��㼴Ϊ����ĵ�M����DΪֱ�Ƕ���ʱ���������������ζ�Ӧ�߳ɱ������CM��Ȼ��д����M�����꼴�ɣ�
��3�����ô���ϵ������һ�κ�������ʽ���ֱ��BD�Ľ���ʽ�������P��y��ƽ�е�ֱ����ֱ��BD�ཻ�ڵ�Q����ʾ��PQ�������������ε������ʽ��ƽ���ı��ε������ʽ�г����̣����xֵ��Ȼ�����������߽���ʽ��⼴�ɣ�
����⣺��1���ߵȱߡ�ABC���ŵ�C˳ʱ����ת60��ĵõ���DEF������ת��D��A��E��B��F��C��Ӧ����
���CAD=��ACB=60�㣬
��AD��x�ᣬ
��B��-1��0����C��1��0����
��BC=2��AO=
��2=
��
���A��������0��
������D��������2��
����
�辭��A��B��D����������߽���ʽΪy=ax2+bx+c��
��
��
���
��
���ԣ������߽���ʽΪy=-
x2+
x+
��
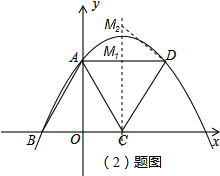
��2����AD��x�ᣬ
���MΪAD��Գ���Ľ���ʱ��CMD=90�㣬
��ʱ��M1��1��
����
����DΪֱ�Ƕ��㣬���CDM1�ס�CM2D��
��
=
��
��
=
��
���CM2=
��
��ʱ����M2��1��
����
����������M1��1��
����M2��1��
��ʱ���Ե�C��D��MΪ�������������ֱ�������Σ�
��3����ֱ��BD�Ľ���ʽΪy=kx+b��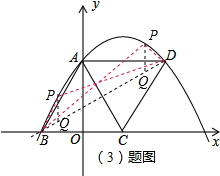
��
��
���
��
���ԣ�y=
x+
��
�����P��y��ƽ�е�ֱ����ֱ��BD�ཻ�ڵ�Q��
��PQ=��-
x2+
x+
��-��
x+
��=-
x2+
x+
��
��S��PBD=
S�ı���ABCD��
��
����-
x2+
x+
������2+1��=
��2��
��
�����ã�x2-x-1=0��
���x1=
��x2=
��
���ԣ�y1=
+
��y2=
-
��
���ԣ���P������Ϊ��
��
+
����
��
-
����
���CAD=��ACB=60�㣬
��AD��x�ᣬ
��B��-1��0����C��1��0����
��BC=2��AO=
| ||
| 2 |
| 3 |
���A��������0��
| 3 |
| 3 |
�辭��A��B��D����������߽���ʽΪy=ax2+bx+c��
��
|
���
|
���ԣ������߽���ʽΪy=-
| ||
| 3 |
2
| ||
| 3 |
| 3 |

��2����AD��x�ᣬ
���MΪAD��Գ���Ľ���ʱ��CMD=90�㣬
��ʱ��M1��1��
| 3 |
����DΪֱ�Ƕ��㣬���CDM1�ס�CM2D��
��
| CM1 |
| CD |
| CD |
| CM2 |
��
| ||
| 2 |
| 2 |
| CM2 |
���CM2=
4
| ||
| 3 |
��ʱ����M2��1��
4
| ||
| 3 |
����������M1��1��
| 3 |
4
| ||
| 3 |
��3����ֱ��BD�Ľ���ʽΪy=kx+b��

��
|
���
|
���ԣ�y=
| ||
| 3 |
| ||
| 3 |
�����P��y��ƽ�е�ֱ����ֱ��BD�ཻ�ڵ�Q��
��PQ=��-
| ||
| 3 |
2
| ||
| 3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
��S��PBD=
| 1 |
| 4 |
��
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 4 |
| 3 |
�����ã�x2-x-1=0��
���x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
���ԣ�y1=
| ||
| 6 |
5
| ||
| 6 |
5
| ||
| 6 |
| ||
| 6 |
���ԣ���P������Ϊ��
1+
| ||
| 2 |
| ||
| 6 |
5
| ||
| 6 |
1-
| ||
| 2 |
5
| ||
| 6 |
| ||
| 6 |
�����������Ƕ��κ����ۺ��⣬��Ҫ��������ת�����ʣ��ȱ������ε����ʣ�����ϵ��������κ�������ʽ������ϵ������һ�κ�������ʽ��ֱ�������ε����ʣ��ѵ����ڣ�2��Ҫ��������ۣ���3����ʾ����PBD�������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��ͼ����AB��OC������Ϊ��C������OA����OC=2��AB=4����OA���ڣ�������
��ͼ����AB��OC������Ϊ��C������OA����OC=2��AB=4����OA���ڣ�������A��2
| ||
B��2
| ||
C��3
| ||
D��2
|
����ʽ-
��
��x+y��
��
��
��
���Ƿ�ʽ���У�������
| 3x |
| 2 |
| 4 |
| x-y |
| x2+1 |
| �� |
| 7 |
| 8 |
| 5b |
| 3a |
| x2 |
| x |
| A��1�� | B��2�� | C��3�� | D��4�� |
���θ�ʽ
������ʱ��x��ȡֵ��Χ�ǣ�������
| x+3 |
| A��x��-3 | B��x��-3 |
| C��x��-3 | D��x��-3 |
��ijһʱ�̣����һ����Ϊ1.8m����͵�Ӱ��Ϊ3m��ͬʱ���һ����˵�Ӱ��Ϊ25m����ô�����˵ĸ߶�Ϊ��������
| A��10m | B��12m |
| C��15m | D��40m |
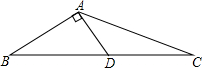 ��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ���AD��AB��AB=3��AC=5����AD�ij���
��ͼ���ڡ�ABC�У�AD��BC���ϵ����ߣ���AD��AB��AB=3��AC=5����AD�ij���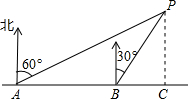 ��ͼ��С��ͬѧ�ڶ�������Ļ���·A������ú��е���P�����ı�ƫ��60�㷽���ϣ���A������400��B������ú��е���P�����ı�ƫ��30�㷽���ϣ��ʣ�����P������·�ľ���PCԼ���ڶ����ף���
��ͼ��С��ͬѧ�ڶ�������Ļ���·A������ú��е���P�����ı�ƫ��60�㷽���ϣ���A������400��B������ú��е���P�����ı�ƫ��30�㷽���ϣ��ʣ�����P������·�ľ���PCԼ���ڶ����ף���