题目内容
8.某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,所以企业规定销售单价不得高于100元,但又不能低于成本.(1)求出每天的销售利润y(元)与销售单价x(元)之间的函数关系式,并写出自变量的取值范围;
(2)求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
分析 (1)根据“利润=(售价-成本)×销售量”列出函数解析式即可;
(2)把(1)中的二次函数解析式转化为顶点式方程,利用二次函数图象的性质进行解答.
解答 解:(1)y=(x-50)[50+5(100-x)]
=(x-50)(-5x+550)
=-5x2+800x-27500
所以y=-5x2+800x-27500(50≤x≤100);
(2)y=-5x2+800x-27500
=-5(x-80)2+4500
∵a=-5<0,
∴抛物线开口向下.
∵50≤x≤100,对称轴是直线x=80,
∴当x=80时,y最大值=4500;
即销售单价为80元时,每天的销售利润最大,最大利润是4500元.
点评 此题考查二次函数的实际运用,掌握销售问题中的基本数量关系得出函数解析式是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
19.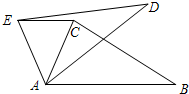 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
13.甲、乙两名队员在相同的条件下各射击10次,每次命中的环数如下表所示:
(1)甲、乙两名队员的射击成绩的平均成绩相等,请补齐甲的成绩;
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲 | 8 | 6 | 7 | 8 | 9 | 10 | 6 | 5 | 4 | 7 |
| 乙 | 7 | 9 | 8 | 5 | 6 | 7 | 7 | 6 | 7 | 8 |
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
20.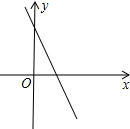 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )| A. | m>n | B. | m<n | C. | m≥n | D. | m≤n |
18. 如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
 如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )
如图,OA=OB,OC=OD,∠D=35°,则∠C等于( )| A. | 60° | B. | 50° | ||
| C. | 35° | D. | 条件不够,无法求出 |
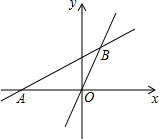 如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.
如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.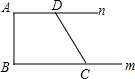 如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.
如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$. 二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是-1<x<3.
二次函数y=ax2+bx+c的图象如图所示,当函数值y<0时,自变量x的取值范围是-1<x<3.