题目内容
19.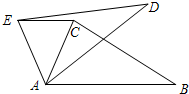 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
分析 根据旋转的性质得AC=AE,∠BAD=∠CAE,再利用等腰三角形的性质得∠ACE=∠AEC,接着根据平行线的性质由EC∥AB得到∠ACE=∠CAB=65°,则可根据三角形内角和定理计算出∠CAE=50°,从而得到∠BAD=50°.
解答 解:∵△ABC绕点A逆时针旋转到△ADE的位置,
∴AC=AE,∠BAD=∠CAE,
∴∠ACE=∠AEC,
∵EC∥AB,
∴∠ACE=∠CAB=65°,
∴∠CAE=180°-65°-65°=50°,
∴∠BAD=50°.
故选A.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决本题的关键是判断△PCE为等腰三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知点(-2,2)在二次函数y=ax2上,那么a的值是( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
7.下列各选项的两个图形(实线部分),不属于位似图形的是( )
| A. |  | B. |  | C. |  | D. |  |
14.如图,在“妙手推推推”的游戏中,主持人出示了一个9位数,让参加者猜商品价格.被猜的价格是一个4位数,也就是这个9位中从左到右连在一起的某4个数字.如果参与者不知道商品的价格,从这些连在一起的所有4位数中,任意猜一个,求他猜中该商品价格的概率( )

| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
9.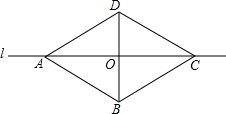 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
 如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )
如图,四边形ABCD沿直线l对折后重合,如果AD∥BC,则结论①AB∥CD;②AB=CD;③AC⊥BD;④AO=CO中正确的是( )| A. | ①②③④ | B. | ①③④ | C. | ②③④ | D. | ③④ |
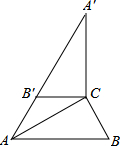 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为6.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为6.