题目内容
16．
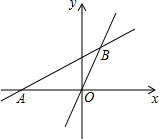如图，直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A，与直线y=2x交于点B．（1）求点B的坐标；
（2）求△AOB的面积．
分析 （1）联立两个方程进行解答即可；
（2）根据三角形的面积公式计算即可．
解答 解：（1）联立两个方程可得：$\left\{\begin{array}{l}{y=2x}\\{y=\frac{1}{2}x+\frac{3}{2}}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$，
所以点B的坐标为（1，2）；
（2）把y=0代入y=$\frac{1}{2}x+\frac{3}{2}$中，可得：x=-3，
所以△AOB的面积=$\frac{1}{2}×3×2=3$．
点评 本题主要考查了两条直线相交的问题，关键是根据两条直线相交时交点为方程组的解进行解答．
练习册系列答案
相关题目
7．下列各选项的两个图形（实线部分），不属于位似图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
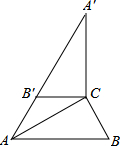如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为6．
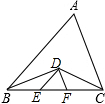如图所示，在△ABC中，BD、CD分别是∠ABC、∠ACB的平分线，DE∥AB，DF∥AC，若△DEF的周长为100cm，则BC的长为100cm．
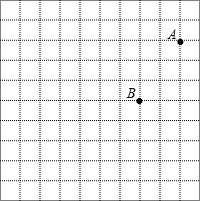如图是由边长为1的小正方形组成的方格图．