题目内容
12.已知样本甲的平均数${\overline x_甲}$=60,方差$s_甲^2$=0.05,样本乙的平均数${\overline x_乙}$=60,方差$s_乙^2$=0.1,那么这两组数据的波动情况为( )| A. | 甲、乙两样本波动一样大 | B. | 甲样本的波动比乙样本大 | ||
| C. | 乙样本的波动比甲样本大 | D. | 无法比较两样本波动的大小 |
分析 根据方差的意义可作出判断.方差是用来衡量一组数据波动大小的量,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
解答 解:∵${\overline x_甲}$=60,${\overline x_乙}$=60,$s_甲^2$=0.05,$s_乙^2$=0.1,
∴$s_甲^2$<$s_乙^2$,
∴乙样本的波动比甲样本大;
故选C.
点评 本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.已知△ABC的三边长分别为4,3,6,与它相似的△DEF的最小边长为12,则△DEF的周长为( )
| A. | 39 | B. | 26 | C. | 52 | D. | 13 |
20.下列各式计算结果中正确的是( )
| A. | a2+a2=a4 | B. | (-2x2)2=-4x4 | C. | (a+1)2=a2+1 | D. | a•a=a2 |
17.在?ABCD中,对角线AC与BD相交于点O,若AC=8,BD=6,则边长AB的取值范围是( )
| A. | 1<AB<7 | B. | 2<AB<14 | C. | 6<AB<8 | D. | 3<AB<4 |
4.已知等腰三角形的周长为24,腰长为x,则x的取值范围是( )
| A. | x>12 | B. | x<6 | C. | 6<x<12 | D. | 0<x<12 |
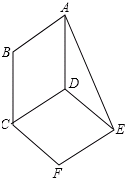 如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.
如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.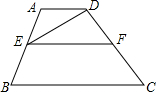 如图,∵∠ADE=∠DEF(已知),
如图,∵∠ADE=∠DEF(已知),