题目内容
2.已知△ABC的三边长分别为4,3,6,与它相似的△DEF的最小边长为12,则△DEF的周长为( )| A. | 39 | B. | 26 | C. | 52 | D. | 13 |
分析 由△ABC的三边长分别为4,3,6,与它相似的△DEF的最小边长为12,即可求得△AC的周长以及相似比,又由相似三角形的周长的比等于相似比,即可求得答案.
解答 解:∵△ABC的三边长分别为4,3,6,
∴△ABC的周长为:4+3+6=13,
∵与它相似的△DEF的最小边长为12,
∴△DEF的周长:△ABC的周长=12:3=4:1,
∴△DEF的周长为:4×13=52.
故选C.
点评 此题考查了相似三角形的性质.注意相似三角形的周长比等于相似比.

练习册系列答案
相关题目
18.在平行四边形、正方形、正五边形、正六边形四个图形中是中心对称图形的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.已知样本甲的平均数${\overline x_甲}$=60,方差$s_甲^2$=0.05,样本乙的平均数${\overline x_乙}$=60,方差$s_乙^2$=0.1,那么这两组数据的波动情况为( )
| A. | 甲、乙两样本波动一样大 | B. | 甲样本的波动比乙样本大 | ||
| C. | 乙样本的波动比甲样本大 | D. | 无法比较两样本波动的大小 |
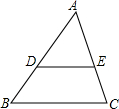 如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长.
如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长.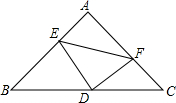 在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.