题目内容
7．若3xm+3y2n与2x2m-2yn+1为同类项，则m=5．分析 由同类项的定义可知，x，y的指数分别相同，即m+3=2m-2，2n=n+1，求出m，n的值．
解答 解：∵3xm+3y2n与2x2m-2yn+1为同类项，
∴m+3=2m-2，2n=n+1，
∴m=5，n=1，
故答案为：5．
点评 此题考查了同类项，熟练掌握同类项的定义是解本题的关键．
练习册系列答案
金钥匙试卷系列答案
相关题目
2．将抛物线y=x2向上平移3个单位，再向左平移2个单位，那么得到的抛物线解析式为（ ）
| A． | y=（x-2）2+3 | B． | y=（x+2）2+3 | C． | y=（x+2）2-3 | D． | y=（x-2）2-3 |
12．已知样本甲的平均数${\overline x_甲}$=60，方差$s_甲^2$=0.05，样本乙的平均数${\overline x_乙}$=60，方差$s_乙^2$=0.1，那么这两组数据的波动情况为（ ）
| A． | 甲、乙两样本波动一样大 | B． | 甲样本的波动比乙样本大 | ||
| C． | 乙样本的波动比甲样本大 | D． | 无法比较两样本波动的大小 |
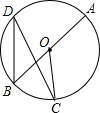如图，AB是⊙O的直径，点C，D是圆上两点，∠AOC=120°，则∠D=30°．