题目内容
2.在△ABC中,∠A+∠B=100°,∠C=4∠A,则∠A=20°,∠C=80°.分析 先根据三角形内角和定理求出∠C的度数,再由∠C=4∠A求出∠A的度数即可.
解答 解:∵∠A+∠B=100°,
∴∠C=180°-100°=80°.
∵∠C=4∠A,
∴∠A=20°.
故答案为:20°,80°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
12.已知样本甲的平均数${\overline x_甲}$=60,方差$s_甲^2$=0.05,样本乙的平均数${\overline x_乙}$=60,方差$s_乙^2$=0.1,那么这两组数据的波动情况为( )
| A. | 甲、乙两样本波动一样大 | B. | 甲样本的波动比乙样本大 | ||
| C. | 乙样本的波动比甲样本大 | D. | 无法比较两样本波动的大小 |
10.某社区购甲乙两种树苗共500棵,甲乙两种树苗单价及成活率见下表:
(1)设购买树苗的费用为y元,购买甲种树苗的数量为x棵,则y与x的函数关系式为:y=-10x+20000;
(2)该社区要同时种植甲乙两种树苗,又希望购进的这批树苗成活率不低于90%,并使购买树苗的费用最低,那么应如何选购树苗.
| 种类 | 单价 | 成活率 |
| 甲 | 30 | 86% |
| 乙 | 40 | 96% |
(2)该社区要同时种植甲乙两种树苗,又希望购进的这批树苗成活率不低于90%,并使购买树苗的费用最低,那么应如何选购树苗.
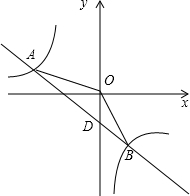 在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.
在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.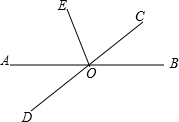 如图,已知直线AB、CD相交于点O,OE平分∠AOC,若∠AOD=30°,求∠BOE的度数.
如图,已知直线AB、CD相交于点O,OE平分∠AOC,若∠AOD=30°,求∠BOE的度数.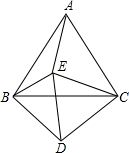 如图,△ABC和△CDE都是等边三角形,且∠EBD=66°,则∠AEB的大小=126°.
如图,△ABC和△CDE都是等边三角形,且∠EBD=66°,则∠AEB的大小=126°.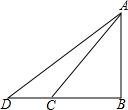 如图,小山岗的斜坡AC的坡角45°,在与山脚C距离200米的D处,测得山顶A的仰角为30°,即∠ACB=45°,∠ADB=30°,求小山岗的高AB.
如图,小山岗的斜坡AC的坡角45°,在与山脚C距离200米的D处,测得山顶A的仰角为30°,即∠ACB=45°,∠ADB=30°,求小山岗的高AB.