题目内容
3.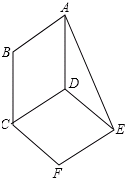 如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.
如图,平行四边形ABCD与平行四边形DCFE的周长相等,且∠BAD=60°,∠F=110°,BC=6.(1)求边CF的长;
(2)求∠DAE的度数.
分析 (1)由平行四边形ABCD与平行四边形DCFE的周长相等,根据平行四边形的对边相等,易得CF=BC=6;
(2)由∠BAD=60°,∠F=110°,可求得∠ADC=180°-∠BAD=120°,∠CDE=∠F=110°,继而求得∠ADE的度数,然后由等腰三角形的性质,求得答案.
解答 解:(1)∵四边形ABCD与四边形DCFE是平行四边形,
∴BC=AD,CF=DE,AB=CD=EF,
∵平行四边形ABCD与平行四边形DCFE的周长相等,
∴CF=BC=6;
(2)∵平行四边形ABCD与平行四边形DCFE中,∠BAD=60°,∠F=110°,
∴∠ADC=180°-∠BAD=120°,∠CDE=∠F=110°,
∴∠ADE=360°-∠ADC-∠CDE=130°,
∵AD=DE=BC=CF,
∴∠DAE=$\frac{1}{2}$(180°-∠ADE)=25°.
点评 此题考查了平行四边形的性质以及等腰三角形的性质.注意掌握平行四边形的对角相等,邻角互补,对边相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知样本甲的平均数${\overline x_甲}$=60,方差$s_甲^2$=0.05,样本乙的平均数${\overline x_乙}$=60,方差$s_乙^2$=0.1,那么这两组数据的波动情况为( )
| A. | 甲、乙两样本波动一样大 | B. | 甲样本的波动比乙样本大 | ||
| C. | 乙样本的波动比甲样本大 | D. | 无法比较两样本波动的大小 |
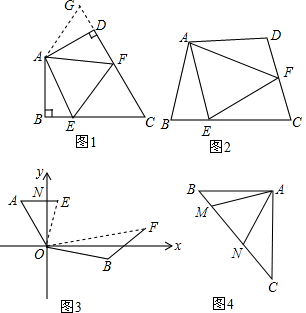
 在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.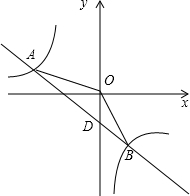 在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.
在平面直角坐标系中,O为原点,一次函数与反比例函数相交于A(-3,1),B(1,-3)两点,连接OA,OB,直线与y轴交于点D.