题目内容
17.在?ABCD中,对角线AC与BD相交于点O,若AC=8,BD=6,则边长AB的取值范围是( )| A. | 1<AB<7 | B. | 2<AB<14 | C. | 6<AB<8 | D. | 3<AB<4 |
分析 由在?ABCD中,对角线AC与BD相交于点O,若AC=8,BD=6,根据平行四边形的对角线互相平分,可求得OA与OB的长,然后由三角形三边关系,求得答案.
解答 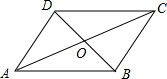 解:∵在?ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,
解:∵在?ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,
∴OA=$\frac{1}{2}$AC=4,OB=$\frac{1}{2}$BD=3,
∴边长AB的取值范围是:1<AB<7.
故选A.
点评 此题考查了平行四边形的性质以及三角形三边关系.注意平行四边形的对角线互相平分.

练习册系列答案
相关题目
5.下列叙述中,正确的是( )
| A. | 方程是含有未知数的式子 | B. | 方程是等式 | ||
| C. | 只有含有字母x,y的等式才叫方程 | D. | 带等号和字母的式子叫方程 |
12.已知样本甲的平均数${\overline x_甲}$=60,方差$s_甲^2$=0.05,样本乙的平均数${\overline x_乙}$=60,方差$s_乙^2$=0.1,那么这两组数据的波动情况为( )
| A. | 甲、乙两样本波动一样大 | B. | 甲样本的波动比乙样本大 | ||
| C. | 乙样本的波动比甲样本大 | D. | 无法比较两样本波动的大小 |
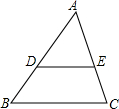 如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长.
如图所示,D,E是△ABC的边AB,AC上的两点,AE:AC=2:3,且AD=10,AB=15,DE=8,求BC的长.