题目内容
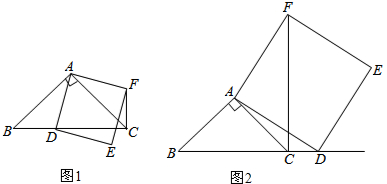
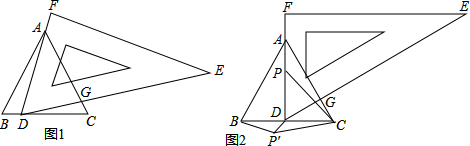
13.在△ABC中,∠ACB为锐角,点D为BC所在直线上一点,连结AD,以AD为边,在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图1,线段CF、BD所在直线的关系为CF⊥BD;
②当点D在线段BC的延长线上时,如图2,①中的结论是否成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F不重合),并说明理由.
(3)在(2)的条件下,若AC=$\sqrt{2}$m,设正方形ADEF的边DE与线段CF相交于点P,当线段CP长的最大时,求CD的值.
分析 (1)①证明△ABD≌△ACF,即可证明∠ACF=∠B,从而证得CF⊥BD;
②与①相同,证明△DAB≌△FAC,证明∠ACF=∠B,从而证得CF⊥BD;
(2)过点A作AG⊥AC交CB或CB的延长线于点G,(1)①可知CF⊥BD;
(3)作AG⊥BC于G,证明△ADQ∽△DPC,根据相似三角形的对应边的比相等,即可求解.
解答 解:(1)①垂直.
理由是:∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF,
则在△ABD和△ACF中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△ABD≌△ACF,
∴∠ACF=∠B,
又∵在直角△ABC中,∠B+∠ACB=90°,
∴∠ACF+∠ACB=90°,即∠BCF=90°,
∴CF⊥BC.
故答案是:CF⊥BC;
②当点D在BC的延长线上时①的结论仍成立.
证明:如图,由正方形ADEF得: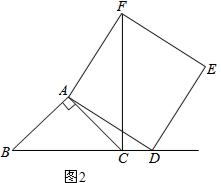
AD=AF,∠DAF=90°.
∵∠BAC=90°,
∴∠DAF=∠BAC,
∴∠DAB=∠FAC,
又AB=AC,
在△ABD和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAF}\\{AD=AF}\end{array}\right.$,
∴△DAB≌△FAC,
∴CF=BD,∠ACF=∠ABD.
∵∠BAC=90°,AB=AC,
∴∠ABC=45°,
∴∠ACF=45°,
∴∠BCF=∠ACB+∠ACF=90°.
即 CF⊥BD.
(2)当∠ACB=45°时,CF⊥BD(如图3).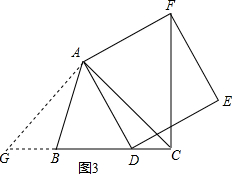
理由:过点A作AG⊥AC交CB或CB的延长线于点G,
则∠GAC=90°,
∵∠ACB=45°,
∠AGC=90°-∠ACB=45°,
∴∠ACB=∠AGC,
∴AC=AG,
∵点D在线段BC上,
∴点D在线段GC上,由(1)①可知CF⊥BD.
(3)如图4:作AG⊥BC于G.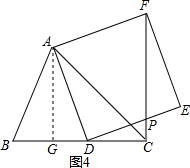
∵∠ACB=45° AC=$\sqrt{2}$m
∴CQ=AQ=m,
∵∠PCD=∠ADP=90°
∴∠ADQ+∠CDP=∠CDP+∠CPD=90°
∴△ADQ∽△DPC,
∴$\frac{PC}{DG}=\frac{CD}{AG}$
设CD为x则DG=CG-CD=m-x 则$\frac{PC}{m-x}=\frac{x}{m}$
∴PC=$\frac{1}{m}(-{x^2}+mx)=-\frac{1}{m}{(x-\frac{m}{2})^2}+\frac{m}{4}$
∴当x=$\frac{m}{2}$时,PC最长,此时PC=$\frac{m}{4}$,
即PC最长时,CD的长为$\frac{m}{2}$.
点评 本题考查了全等三角形的判定与性质以相似三角形的判定与性质,正确作出辅助线,理解每个小题之间的联系是关键.


 设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证:
设G是△ABC的重心,M是边AC的中点,且AC=2$\sqrt{3}$GM,D是GA延长线上任一点,连接DM,并在DM上取一点E,使∠AED=∠CAG,作CF∥AB与直线BE交于点F,CD与MF交于点H,求证: