题目内容
5.先阅读,再解答问题例:解不等式$\frac{1-x}{2x-1}$>0
解:则有(1)$\left\{\begin{array}{l}{1-x>0}\\{2x-1>0}\end{array}\right.$ 或(2)$\left\{\begin{array}{l}{1-x<0}\\{2x-1<0}\end{array}\right.$
解不等式组(1)得$\frac{1}{2}$<x<1,解不等式组(2)知其无解
所以得不等式的解集为$\frac{1}{2}$<x<1
请根据以上解不等式的思想方法解不等式$\frac{3x+2}{x-2}$<0.
分析 根据题意列出关于x的不等式组,求出x的取值范围即可.
解答 解:∵$\frac{3x+2}{x-2}$<0,
∴$\left\{\begin{array}{l}3x+2>0\\ x-2<0\end{array}\right.$(1)或$\left\{\begin{array}{l}3x+2<0\\ x-2>0\end{array}\right.$(2),
解(1)得-$\frac{2}{3}$<x<2;
解(2)知此不等式组无解.
故不等式组的解集为:-$\frac{2}{3}$<x<2.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
10.下列命题错误的是( )
| A. | 两个角的余角相等,则这两个角相等 | |
| B. | 两条平行线被第三条直线所截内错角的平分线平行 | |
| C. | 无理数包括正无理数,0,负无理数 | |
| D. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 |
 如图,△ABC与△BEF都是等边三角形,D是BC上一点,且CD=BE,求证:∠EDB=∠CAD.
如图,△ABC与△BEF都是等边三角形,D是BC上一点,且CD=BE,求证:∠EDB=∠CAD.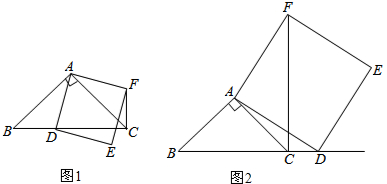
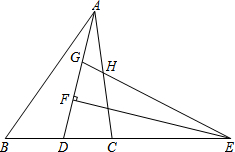 如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.
如图,在△ABC中,AD为△ABC的角平分线,点E在BC的延长线上,EF⊥AD于点F,点G在AF上,FG=FD,连接EG交AC于点H.


