题目内容
5.抛物线y=x2+4x+8关于点(3,1)中心对称之后的抛物线解析式为y=-x2+16x-66.分析 先利用配方法得到抛物线y=x2+4x+8的顶点坐标为(-2,4),再找出点(-2,4)关于点(3,1)对称的对应点的坐标为(8,-2),然后根据顶点式写出对称后的抛物线解析式.
解答 解:∵y=x2+4x+8=(x+2)2+4,
∴该抛物线的顶点坐标为(-2,4),点(-2,4)关于点(3,1)对称的对应点的坐标为(8,-2).
∵由于对称后抛物线开口相反,所以对称后的抛物线解析式为y=-(x-8)2-2,即y=-x2+16x-66.
故答案为y=-x2+16x-66.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
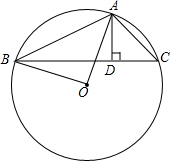 如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度(AD>DC)为方程x2-7x+12=0的两根,⊙O是△ABC的外接圆,如果BD的长为8,求△ABC的外接圆的直径.
如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度(AD>DC)为方程x2-7x+12=0的两根,⊙O是△ABC的外接圆,如果BD的长为8,求△ABC的外接圆的直径.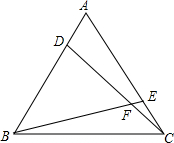 如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数.
如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC与E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC与E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.