题目内容
10. 如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC与E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.
如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC与E,F两点,再分别以E,F为圆心,大于$\frac{1}{2}$EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M.(1)若∠ACD=138°,求∠MAB的度数.
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN.
分析 (1)根据AB∥CD,∠ACD=138°,得出∠CAB=42°,再根据AM是∠CAB的平分线,即可得出∠MAB的度数.
(2)根据∠CAM=∠MAB,∠MAB=∠CMA,得出∠CAM=∠CMA,再根据CN⊥AD,CN=CN,即可得出△ACN≌△MCN.
解答 (1)解:∵AB∥CD,
∴∠ACD+∠CAB=180°,
又∵∠ACD=138°,
∴∠CAB=42°,
由作法知,AM是∠CAB的平分线,
∴∠MAB=$\frac{1}{2}$∠CAB=21°;
(2)证明:∵AM平分∠CAB,
∴∠CAM=∠MAB,
∵AB∥CD,
∴∠MAB=∠CMA,
∴∠CAM=∠CMA,
又∵CN⊥AM,
∴∠ANC=∠MNC,
在△ACN和△MCN中,$\left\{\begin{array}{l}{∠ANC=∠MNC}\\{∠CAM=∠CMA}\\{CN=CN}\end{array}\right.$,
∴△ACN≌△MCN(AAS).
点评 此题考查了作图-复杂作图,用到的知识点是全等三角形的判定、平行线的性质、角平分线的性质等,解题的关键是证出∠CAM=∠CMA.

练习册系列答案
相关题目
15.若|a|=5,|b|=2,a<b,则a,b分别为( )
| A. | 5,-2 | B. | -5,-2 | C. | -5,2 | D. | -5,-2或-5,2 |
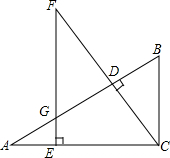 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F,EF交AB于G.求证:
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F,EF交AB于G.求证: 如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.
如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.