题目内容
16.已知a,b,c均为实数,且a+b+c=0,abc=16,求正数c的最小值.分析 由已知条件变形得到a+b=-c,ab=$\frac{16}{c}$,根据根与系数的关系,可把a、b看作方程x2+cx+$\frac{16}{c}$=0的两根,再利用判别式的意义得到c2-4×1×$\frac{16}{c}$≥0,然后解此不等式即可.
解答 解:∵a+b+c=0,abc=16,
∴a+b=-c,ab=$\frac{16}{c}$,
把a、b看作方程x2+cx+$\frac{16}{c}$=0的两根,
∵△=c2-4×1×$\frac{16}{c}$≥0,
∴c3≥64,
∴c≥4.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了判别式的意义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.
如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.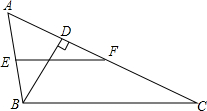 已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB.
已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB.