题目内容
13.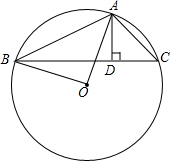 如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度(AD>DC)为方程x2-7x+12=0的两根,⊙O是△ABC的外接圆,如果BD的长为8,求△ABC的外接圆的直径.
如图,在钝角△ABC中,AD⊥BC,垂足为D点,且AD与DC的长度(AD>DC)为方程x2-7x+12=0的两根,⊙O是△ABC的外接圆,如果BD的长为8,求△ABC的外接圆的直径.
分析 延长AO交⊙O于得E,连接BE,解方程求出AD与DC的长度,根据勾股定理求出AC和AB的长度,根据圆周角定理和正弦的定义求出△ABC的外接圆的直径.
解答 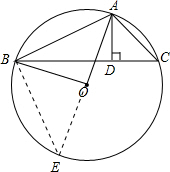 解:延长AO交⊙O于得E,连接BE,
解:延长AO交⊙O于得E,连接BE,
解方程x2-7x+12=0得,x1=3,x2=4,
由题意得,AD=4,DC=3,
由勾股定理得,AC=5,
∵BD=8,
∴AB=$\sqrt{B{D}^{2}+A{D}^{2}}$=4$\sqrt{5}$,
∵sinC=$\frac{AD}{AC}$=$\frac{4}{5}$,又∠E=∠C,
∴sinE=$\frac{AB}{AE}$=$\frac{4}{5}$,AB=4$\sqrt{5}$,
∴AE=5$\sqrt{5}$.
答:△ABC的外接圆的直径是5$\sqrt{5}$.
点评 本题考查的是三角形外接圆与外心的概念和性质以及一元二次方程的解法、勾股定理的应用,正确作出辅助线、解出方程、灵活运用三角形外心的性质是解题的关键.

练习册系列答案
相关题目
 如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.
如图,等腰△ABC中,AC=AE,CE、BF分别为AB、AC的中线,交于点O.猜想AO与BC有什么关系?并说明理由.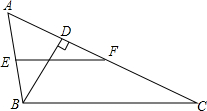 已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB.
已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB.