题目内容
20.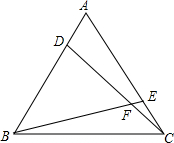 如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数.
如图,D、E分别是等边△ABC的两条边AB、AC上的点,且AD=CE,求∠DFB的度数.
分析 根据等边三角形的性质,结合条件可证明△ADC≌△CEB,可得∠ACD=∠CBE,由∠DFB=∠CBF+∠BCF,可知∠DFB=∠ACB=60°.
解答 证明:∵△ABC为等边三角形,
∴AC=BC,∠A=∠ACB=60°,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{AD=CE}\\{∠A=∠ECB}\\{AC=BC}\end{array}\right.$,
∴△ADC≌△CEB(SAS),
∴∠ACD=∠CBE,
∵∠DFB=∠CBF+∠BCF,
∠ACD+∠BCF=∠ACD,
∴∠DFB=∠ACB=60°.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(SSS、SAS、ASA、AAS和HL)和性质(全等三角形的对应边、对应角相等)是解题的关键.

练习册系列答案
相关题目
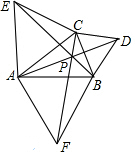 如图,已知△ABC,分别以AC,BC,AB为边,作等边三角形ACE,BCD和ABF,连接AD,BE和CF交于点P,求证:PB+PC+PA=BE.
如图,已知△ABC,分别以AC,BC,AB为边,作等边三角形ACE,BCD和ABF,连接AD,BE和CF交于点P,求证:PB+PC+PA=BE.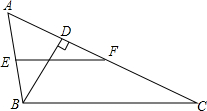 已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB.
已知如图:在ABC中,BD⊥AC,E为AB的中点,EF∥BC,∠A=2∠C,求证:DF=$\frac{1}{2}$AB. 已知有三个数集:A={-1,3.1,-4,6,2.1},B={-4.2,2.1,-1,10,-$\frac{1}{8}$},C={21,-4.2,8,6}
已知有三个数集:A={-1,3.1,-4,6,2.1},B={-4.2,2.1,-1,10,-$\frac{1}{8}$},C={21,-4.2,8,6}