题目内容
4. 如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A. | 60° | B. | 55° | C. | 50° | D. | 45° |
分析 连接OB,OC,先求出∠BAO=25°,进而求出∠OBC=40°,求出∠COE=∠OCB=40°,最后根据等腰三角形的性质,问题即可解决.
解答  解:如图,连接OB,
解:如图,连接OB,
∵∠BAC=50°,AO为∠BAC的平分线,
∴∠BAO=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×50°=25°.
又∵AB=AC,
∴∠ABC=∠ACB=65°.
∵DO是AB的垂直平分线,
∴OA=OB,
∴∠ABO=∠BAO=25°,
∴∠OBC=∠ABC-∠ABO=65°-25°=40°.
∵AO为∠BAC的平分线,AB=AC,
∴直线AO垂直平分BC,
∴OB=OC,
∴∠OCB=∠OBC=40°,
∵将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,
∴OE=CE.
∴∠COE=∠OCB=40°;
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°,
∴∠CEF=$\frac{1}{2}$∠CEO=50°.
故选:C.
点评 该题主要考查了等腰三角形的性质以及翻折变换及其应用,解题的关键是根据翻折变换的性质,找出图中隐含的等量关系,灵活运用有关定理来分析、判断.

练习册系列答案
相关题目
14.下列说法:①球有1个面;②同一平面内的两点,可以确定一条直线;③两点之间,线段最短;④射线没有端点,其中不正确的是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.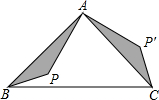 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
12.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{2{x}^{2}}$ | B. | $\sqrt{5}$ | C. | $\sqrt{8}$ | D. | $\sqrt{\frac{1}{x}}$ |
19.下列实数中无理数是( )
| A. | 0 | B. | 3 | C. | π | D. | $\sqrt{4}$ |
16.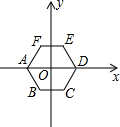 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
 如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )
如图,以半径为2的正六边形ABCDEF的中心O为原点建立平面直角坐标系,顶点A,D在x轴上,则点C的坐标为( )| A. | (1,-2) | B. | (1,-$\sqrt{2}$) | C. | (1,-$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
13.下列说法错误的是( )
| A. | 四边形的内角和与外角和相等 | |
| B. | 五边形的每一个内角都是108° | |
| C. | 六边形的内角和等于其外角和的2倍 | |
| D. | 从n边形的一个顶点出发可以引(n-3)条对角线 |
14. 如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
 如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )| A. | $\frac{2}{5}$$\sqrt{5}$ | B. | $\frac{1}{2}$$\sqrt{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{4}$$\sqrt{13}$ |