题目内容
14. 如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )
如图,锐角△ABC内接于⊙O,AO=3,AC=4,则tanB=( )| A. | $\frac{2}{5}$$\sqrt{5}$ | B. | $\frac{1}{2}$$\sqrt{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{1}{4}$$\sqrt{13}$ |
分析 延长AO交⊙O于D,连接CD,根据圆周角定理求出∠B=∠D,∠ACD=90°,根据勾股定理求出CD,解直角三角形求出即可.
解答 解: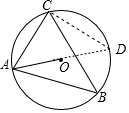
延长AO交⊙O于D,连接CD,
由圆周角定理得:∠B=∠D,∠ACD=90°,
∵AC=4,AO=3=OD,
∴由勾股定理得:CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴tanB=tanD=$\frac{AC}{CD}$=$\frac{4}{2\sqrt{5}}$=$\frac{2}{5}$$\sqrt{5}$,
故选D.
点评 本题考查了勾股定理,圆周角定理,三角形的外接圆与外心的应用,能正确作出辅助线是解此题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
4. 如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
 如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A. | 60° | B. | 55° | C. | 50° | D. | 45° |
5. 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
2. 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
 如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )
如图,已知⊙O的半径为5,弦AB长为8,则点O到弦AB的距离是( )| A. | 2 | B. | 3 | C. | 4 | D. | $\sqrt{17}$ |
6.正六边形的两条对边之间的距离是2$\sqrt{3}$,则它的边长是( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
3.如果a>b,下列各式中不正确的是( )
| A. | -2+a<-2+b | B. | -$\frac{a}{2}$<-$\frac{b}{2}$ | C. | -2a<-2b | D. | a-3>b-3 |
4.现规定一种新运算“*”:a*b=ab,如3*2=32=9,则($\frac{1}{2}$)*3=( )
| A. | $\frac{1}{6}$ | B. | 8 | C. | $\frac{1}{8}$ | D. | $\frac{3}{2}$ |



