题目内容
15.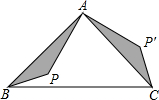 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
分析 根据旋转的性质知:旋转角度是90°,根据旋转的性质得出AP=AP′=4,即△PAP′是等腰直角三角形,腰长AP=4,则可用勾股定理求出斜边PP′的长.
解答 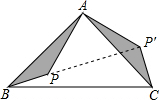 解:连接PP′,
解:连接PP′,
∵△ABP绕点A逆时针旋转后与△ACP′重合,
∴△ABP≌△ACP′,
即线段AB旋转后到AC,
∴旋转了90°,
∴∠PAP′=∠BAC=90°,AP=AP′=4,
∴PP′=$\sqrt{A{P}^{2}+AP{′}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
故选B.
点评 本题考查旋转的性质和直角三角形的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.

练习册系列答案
相关题目
3.下列方程中,解为x=2的方程是( )
| A. | x+2=0 | B. | 2+3x=8 | C. | 3x-1=2 | D. | 4-2x=1 |
10.已知$\frac{c}{4}$=$\frac{b}{5}$=$\frac{a}{6}$≠0,则$\frac{b+c}{a}$的值为( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
20.若双曲线y=$\frac{1-k}{x}$的图象在第一、三象限,则k的取值范围为( )
| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
7.甲队有工人96人,乙队有工人72人,如果要求乙队的人数是甲队人数的$\frac{1}{3}$,应从乙队调 多少人去甲队?如果设应从乙队调x人到甲队,列出的方程正确的是( )
| A. | 96+x=$\frac{1}{3}$(72-x) | B. | $\frac{1}{3}$(96+x)=72-x | C. | $\frac{1}{3}$(96-x)=72-x | D. | $\frac{1}{3}$×96+x=72-x |
4. 如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
 如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )
如图,在等腰△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB的垂直平分线交于点O、点C沿EF折叠后与点O重合,则∠CEF的度数是( )| A. | 60° | B. | 55° | C. | 50° | D. | 45° |
5. 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
 如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )
如图,已知a∥b∥c,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若$\frac{AB}{BC}$=$\frac{1}{2}$,则$\frac{DE}{DF}$的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |