题目内容
19.我校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
分析 (1)根据题意可以分别求得1≤x<50和50≤x≤90时的y与x的函数关系式;
(2)根据题意可以分别求得两段的函数的最大值,从而可以解答本题;
(3)根据题意可以列出相应的不等式,从而可以解答本题.
解答 解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000,
当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000,
综上所述:y=$\left\{\begin{array}{l}{-2{x}^{2}+180x+2000}&{1≤x<50}\\{-120x+12000}&{50≤x≤90}\end{array}\right.$;
(2)当1≤x<50时,
二次函数y=-2x2+180x+2000的图象开口向下,对称轴为x=45,
当x=45时,y最大=-2×452+180×45+2000=6050,
当50≤x≤90时,
y=-120x+12000中y随x的增大而减小,
∴当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)该商品第50天至90天的在销售过程中,共11天每天销售利润不低于4800元,
理由:当50≤x≤90时,
-120x+12000≥4800,
解得x≤60,
∴利润不低于4800元的天数是50≤x≤60,共11天,
即该商品第50天至90天的在销售过程中,共11天每天销售利润不低于4800元.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部,设购进A型手机x部,B型手机y部,三款手机的进价和预售价如表:
(1)请用含x、y的代数式表示购买手机的预售总额,并进行化简;
(2)假设所购进手机恰好用去61000元且全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.请用含x的代数式表示预估利润,并进行化简(注:预估利润P=预售总额-购机款-各种费用).
| 手机型号 | A型 | B型 | C型 |
| 进价(单位:元/部) | 900 | 1200 | 1100 |
| 预售价(单位:元/部) | 1200 | 1600 | 1300 |
(2)假设所购进手机恰好用去61000元且全部售出,综合考虑各种因素,该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.请用含x的代数式表示预估利润,并进行化简(注:预估利润P=预售总额-购机款-各种费用).
16.下列不一定是相似图形的是( )
| A. | 边数相同的正多边形 | B. | 两个等腰直角三角形 | ||
| C. | 两个圆 | D. | 两个等腰三角形 |
 在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.
在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.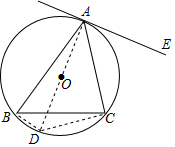 如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.
如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.