题目内容
9.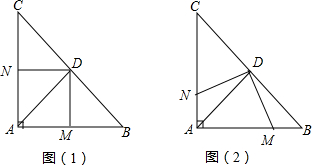 在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.
在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.(1)如图(1),若点M、N分别是线段AB、AC的中点.求证:DM=DN;
(2)如图(2),若点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△DMN的形状,并证明你的结论.
分析 (1)只要证明△AND≌△BMD即可.
(2)结论:△DMN是等腰直角三角形.只要证明△AND≌△BMD,推出DN=DM,∠ADN=∠BDM,由∠ADB=90°,即∠ADM+∠BDM=90°,推出∠ADM+∠ADN=90°,即∠MDN=90°.
解答 证明:(1)如图中,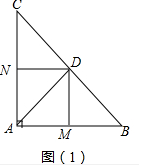
∵AB=AC,∠BAC=90°,
∴∠B=45°,
∵D是斜边BC上的中点
∴AD=BD=$\frac{1}{2}BC$,
又∵AB=AC,AD是底边BC上的中线
∴AD也是∠BAC的平分线,即∠DAN=∠DAB=45°,
∴∠B=∠NAD,
∵AC=AB,M,N分别是线段AB、AC的中点
∴AN=MB
在△AND和△BMD中,
$\left\{\begin{array}{l}{AD=BD}\\{∠NAD=∠B}\\{AN=BM}\end{array}\right.$,
∴△AND≌△BMD,
∴DM=DN.
(2)如图2中,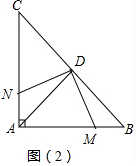
由(1)可知,AD=BD,∠NAD=∠B,
在△AND和△BMD中,
$\left\{\begin{array}{l}{AD=BD}\\{∠NAD=∠B}\\{AN=BM}\end{array}\right.$,
∴△AND≌△BMD,
∴DN=DM,∠ADN=∠BDM,
∵∠ADB=90°,即∠ADM+∠BDM=90°,
∴∠ADM+∠ADN=90°,即∠MDN=90°,
∴△MDN是等腰直角三角形.
点评 本题考查全等三角形的判定和性质、直角三角形斜边中线的性质、等腰直角三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.
3,-(-1),-1.5,0.-|25|,-3.5
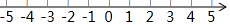
按照从小到大的顺序排列为-3.5<-|-2.5|<-1.5<0<-(-1)<3.
3,-(-1),-1.5,0.-|25|,-3.5
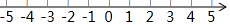
按照从小到大的顺序排列为-3.5<-|-2.5|<-1.5<0<-(-1)<3.
19.我校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
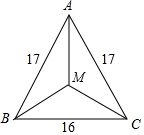 如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,求AM的长度为10.
如图,△ABC中,AB=AC=17,BC=16,M是△ABC的重心,求AM的长度为10.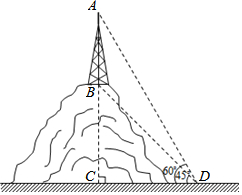 如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).
如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).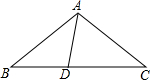 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.