题目内容
11.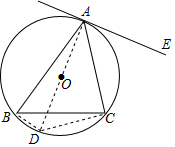 如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.
如图,已知△ABC内接于⊙O,AE为⊙O的切线,求证:∠CAE=∠ABC.
分析 作辅助线,根据切线性质得:OA⊥AE,则∠CAE+∠DAC=90°,由直径所对的圆周角为直角,则∠ABD=90°,即∠ABC+∠DBC=90°,由同角的余角得出结论.
解答 证明:作直径AD,交⊙O于D,连接CD、BD,
∵AE为⊙O的切线,
∴OA⊥AE,
∴∠CAE+∠DAC=90°,
∵AD为⊙O的直径,
∴∠ABD=90°,
∴∠ABC+∠DBC=90°,
∵∠DBC=∠DAC,
∴∠CAE=∠ABC.
点评 本题考查了切线的性质和圆周角定理,圆的切线垂直于过切点的半径,还要知道直径所对的圆周角为直角,且在同圆或等圆中,同弧所对的圆周角相等;在圆中的证明题,常根据这些性质得角的大小关系,因此要熟练掌握.

练习册系列答案
相关题目
19.我校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
7. 如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )
如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )
 如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )
如图,在△ABC中,∠ACB=70°,∠1=∠2,则∠BPC的度数为( )| A. | 110° | B. | 70° | C. | 130° | D. | 不能确定 |
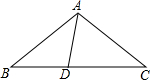 如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC.
如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.求证:AC=DC. 如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.
如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.