题目内容
4.如果方程2xm-1-3y2m+n=1是二元一次方程,那么m=2,n=-3.分析 根据二元一次方程的定义,从二元一次方程的未知数的个数和次数方面考虑求常数m、n的值.
解答 解:根据二元一次方程的定义,得:$\left\{\begin{array}{l}{m-1=1}\\{2m+n=1}\end{array}\right.$,
解这个方程组,得:$\left\{\begin{array}{l}{m=2}\\{n=-3}\end{array}\right.$.
故答案为:2,-3.
点评 本题考查了二元一次方程的定义,注意二元一次方程必须符合以下三个条件:(1)方程中只含有2个未知数;(2)含未知数项的最高次数为一次;(3)方程是整式方程.

练习册系列答案
相关题目
14.在数轴上表示下列各数,并用“<”号把它们按照从小到大的顺序排列.
3,-(-1),-1.5,0.-|25|,-3.5
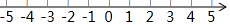
按照从小到大的顺序排列为-3.5<-|-2.5|<-1.5<0<-(-1)<3.
3,-(-1),-1.5,0.-|25|,-3.5
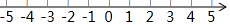
按照从小到大的顺序排列为-3.5<-|-2.5|<-1.5<0<-(-1)<3.
19.我校九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在第50天至90天的销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
 如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.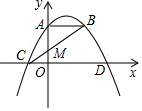 如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D.
如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D. 如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.
如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.