题目内容
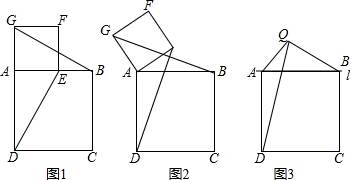
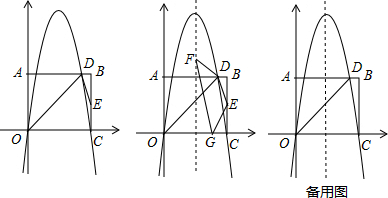
14.【观察发现】(1)如图1,四边形ABCD和四边形AEFG都是正方形,且点E在边AB上,连接DE和BG,猜想线段DE与BG的数量关系和位置关系.(只要求写出结论,不必说出理由)【深入探究】(2)如图2,将图1中正方形AEFG绕点A逆时针旋转一定的角度,其他条件与观察发现中的条件相同,观察发现中的结论是否还成立?请根据图2加以说明.
【拓展应用】(3)如图3,直线l上有两个动点A、B,直线l外有一点动点Q,连接QA,QB,以线段AB为边在l的另一侧作正方形ABCD,连接QD.随着动点A、B的移动,线段QD的长也会发生变化,若QA,QB长分别为$3\sqrt{2}$,6保持不变,在变化过程中,线段QD的长是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
分析 (1)根据正方形的性质,由SAS证明△BAG≌△DAE,得出DE=BG,∠ABG=∠ADE,再由角的互余关系证出DE⊥BG即可;
(2)同(1)证明△BAG≌△DAE,从而证明结论;
(3)以OA为边作正方形QAGF,连接QG、BG,则QC=$\sqrt{2}$OA=4,当G、Q、B三点共线时,BG最长,此时BC=QC+QB=8,从而得出答案.
解答 (1)解: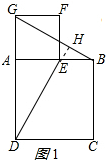 DE=BG,DE⊥BG;理由如下:
DE=BG,DE⊥BG;理由如下:
延长DE交BG于H,如图1所示:
∵四边形ABCD、四边形AEFG都是正方形,
∴AB=AD,AG=AE,∠EAD=∠BAG=90°,
在△BAG与△DAE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAG=∠EAD}&{\;}\\{AG=AE}&{\;}\end{array}\right.$,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE,
∵∠AGB+∠ABG=90°,
∴∠AGB+∠ADE=90°,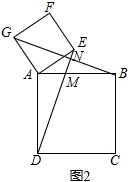
∴∠DHG=90°,
∴DE⊥BG;
(2)解:(1)中的结论成立,即DE=BG,DE⊥BG;
理由如下:如图2所示,
∵四边形ABCD、四边形AEFG都是正方形,
∴BA=AD,AG=AE,∠BAD=∠EAG=90°,
∴∠BAG+∠BAE=∠EAG+∠BAE,
即∠BAG=∠DAE,在△BAG与△DAE中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAG=∠EAD}&{\;}\\{AG=AE}&{\;}\end{array}\right.$,
∴△BAG≌△DAE(SAS),
∴DE=BG,∠ABG=∠ADE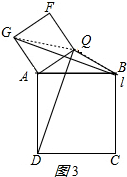
∵∠AMD+∠ADE=90°,∠AMD=∠BME,
∴∠BME+∠ABG=90°,
∴∠DNB=90°,
∴DE⊥BG;
(3)解:QD存在最大值;理由如下:
以QA为边作正方形QAGF,连接QG、BG,如图3所示:
则QG=$\sqrt{2}$QA=4,
由(2)可得:QD=BG,
当G、Q、B三点共线时,BG最长,
此时BC=QG+QB=4+4=8,
即线段QD长的最大值为8.
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、角的互余关系、对顶角相等、三点共线等知识;本题综合性强,证明三角形全等是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案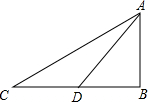 如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )
如图,从地面上C、D两处望山顶A,仰角分别为30°和45°,若C、D两处相距200米,则山高AB为( )| A. | 100($\sqrt{3}$+1)米 | B. | 100米 | C. | 100$\sqrt{2}$ | D. | 200$\sqrt{3}$ |
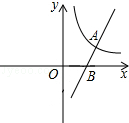 如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.
如图,直线y=2x-6与反比例函数y=$\frac{k}{x}$(k>0)的图象交于点A(4,2),与x轴交于点B.