Question

2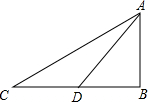．如图，从地面上C、D两处望山顶A，仰角分别为30°和45°，若C、D两处相距200米，则山高AB为（　　）

• A． 100（$\sqrt{3}$+1）米
• B． 100米
• C． 100$\sqrt{2}$
• D． 200$\sqrt{3}$

Answer 1

分析 设山高AB为x，根据∠ADB=45°可得出AB=BD=x，在Rt△ABC中，根据锐角三角函数的定义即可得出结论．

解答 解：设山高AB为x，
∵∠ADB=45°，
∴AB=BD=x，
在Rt△ABC中，
∵∠ACB=30°，
∴$\frac{AB}{BC}$=tan30°，即$\frac{x}{200+x}$=$\frac{\sqrt{3}}{3}$，解得x=100（$\sqrt{3}$+1）米．
故选A．

点评 本题考查的是解直角三角形的应用-方向角问题，熟记锐角三角函数的定义是解答此题的关键．