��Ŀ����
9����ͼ����ƽ��ֱ������ϵ�У�����OABC�ı�OA��y����������ϣ�OC��x����������ϣ���AOC��ƽ���߽�AB�ڵ�D��EΪBC���е㣬��֪A��0��4����C��5��0�����κ���y=ax2+bx��ͼ��D��C����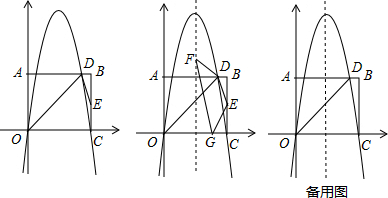
��1����ö��κ����ı���ʽ��
��2��F��G�ֱ�Ϊ�Գ��ᡢx���ϵĶ��㣬��β˳������D��E��G��F�����ı���DEGF�����ı���DEGF�ܳ�����Сֵ��
��3�������ߵĶԳ������Ƿ���ڵ�P��ʹ��ODPΪ���������Σ������ڣ�ֱ��д����P�����꣬�������ڣ���˵�����ɣ�
���� ��1�������á�AOC��ƽ���߽�AB�ڵ�D�õ�AO=AD����D��4��4����Ȼ�����ô���ϵ�����������߽���ʽ��
��2�����ö��κ��������ʵõ������ߵĶԳ���Ϊֱ��x=$\frac{5}{2}$����������AB����һ������ΪD�䣬��E����x��ĶԳƵ�ΪE�䣬����D��E�佻x����G����ֱ��x=-$\frac{5}{2}$��F����ͼ1����������֮���߶�����жϴ�ʱEG+FG+FD��ֵ��С�������ж��ı���DEGF�ܳ�����Сֵ�������D���E�������꣬Ȼ�����������ľ��빫ʽ���D��E���DE���Ӷ��õ��ı���DEGF�ܳ�����Сֵ��
��3��ֱ��x=$\frac{5}{2}$��x���ڵ�H����AB��N����ͼ2�����ù��ɶ��������OD=4$\sqrt{2}$���������ۣ���DG��x���ڵ�G������AG���Գ����ڵ�P1����ͼ2�����ı���AOGDΪ�����Σ���AG��ֱƽ��OD�����ԡ�P1ODΪ���������Σ���ֱ��AG�Ľ���ʽΪy=-x+4����ֱ��y=-x+4��Գ���Ľ���õ�P1�����ꣻ�Ե�DΪԲ�ģ�DOΪ�뾶�������Գ����ڵ�P2��P3����ͼ2����DP2=DP3=4$\sqrt{2}$�����ù��ɶ��������P2N=$\frac{\sqrt{119}}{2}$��ͬ���ɵ�P3N=$\frac{\sqrt{119}}{2}$����ɵõ�P2��P3�����ꣻ�Ե�OΪԲ�ģ�ODΪ�뾶�������Գ����ڵ�P4��P5����ͼ2����OP4=OP5=4$\sqrt{2}$�����ù��ɶ��������P4H��P5H�ij������ǿɵõ�P4��P3�����꣮
��� �⣺��1����A��0��4����C��5��0����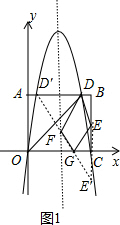
��OA=4��OC=5��
�ߡ�AOC��ƽ���߽�AB�ڵ�D��
��AO=AD��
��D��4��4����
��D��4��4����C��5��0������y=ax2+bx��$\left\{\begin{array}{l}{16a+4b=4}\\{25a+5b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{a=-1}\\{b=5}\end{array}\right.$��
�������߽���ʽΪy=-x2+5x��
��2����y=-x2+5x=-��x-$\frac{5}{2}$��2+$\frac{25}{4}$��
�������ߵĶԳ���Ϊֱ��x=$\frac{5}{2}$��
��������AB����һ������ΪD�䣬��E����x��ĶԳƵ�ΪE�䣬����D��E�佻x����G����ֱ��x=-$\frac{5}{2}$��F����ͼ1��
��FD=FD�䣬GE=GE�䣬
��EG+FG+FD=GE��+FG+FD��=D��E�䣬
���ʱEG+FG+FD��ֵ��С����ʱ�ı���DEGF�ܳ�����Сֵ��
��y=4ʱ��-x2+5x=4�����x1=1��x2=4����D�䣨1��4����
�ߵ�EΪBC���е㣬
��E��5��2����
�ߵ�E�����E����x��Գƣ�
��E�䣨5��-2����
��D��E��=$\sqrt{��1-5��^{2}+��4+2��^{2}}$=2$\sqrt{13}$��DE=$\sqrt{��4-5��^{2}+��4-2��^{2}}$=$\sqrt{5}$��
���ı���DEGF�ܳ�����Сֵ=DE+D��E��=$\sqrt{5}$+2$\sqrt{13}$��
��3�����ڣ�
ֱ��x=$\frac{5}{2}$��x���ڵ�H����AB��N����ͼ2��
��D��4��4����
��OD=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$��
��DG��x���ڵ�G������AG���Գ����ڵ�P1����ͼ2��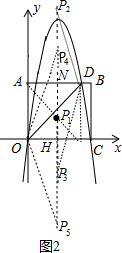
���ı���AOGDΪ�����Σ�
��AG��ֱƽ��OD��
��P1O=P1D������P1OD����������
��G��4��0����
��ֱ��AG�Ľ���ʽΪy=-x+4��
��x=$\frac{5}{2}$ʱ��y=-x+4=$\frac{3}{2}$����P1��$\frac{5}{2}$��$\frac{3}{2}$����
�Ե�DΪԲ�ģ�DOΪ�뾶�������Գ����ڵ�P2��P3����ͼ2����DP2=DP3=4$\sqrt{2}$��
��Rt��DP2N��DN=4-$\frac{5}{2}$=$\frac{3}{2}$��
��P2N=$\sqrt{��4\sqrt{2}��^{2}-��\frac{3}{2}��^{2}}$=$\frac{\sqrt{119}}{2}$��
ͬ���ɵ�P3N=$\frac{\sqrt{119}}{2}$��
��P2��$\frac{5}{2}$��4+$\frac{\sqrt{119}}{2}$����P3��$\frac{5}{2}$��4-$\frac{\sqrt{119}}{2}$����
�Ե�OΪԲ�ģ�ODΪ�뾶�������Գ����ڵ�P4��P5����ͼ2����OP4=OP5=4$\sqrt{2}$��
��Rt��OP4H��P4H=$\sqrt{��4\sqrt{2}��^{2}-��\frac{5}{2}��^{2}}$=$\frac{\sqrt{103}}{2}$��
ͬ���ɵ�P5H=$\frac{\sqrt{103}}{2}$��
��P4��$\frac{5}{2}$��$\frac{\sqrt{103}}{2}$����P3��$\frac{5}{2}$��-$\frac{\sqrt{103}}{2}$����
��������������������P��������$\frac{5}{2}$��$\frac{3}{2}$����$\frac{5}{2}$��4+$\frac{\sqrt{119}}{2}$����$\frac{5}{2}$��4-$\frac{\sqrt{119}}{2}$������$\frac{5}{2}$��$\frac{\sqrt{103}}{2}$����$\frac{5}{2}$��-$\frac{\sqrt{103}}{2}$����
���� ��ͬ�����˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ���������������κ��������ʺ͵��������ε��ж��������ô���ϵ������������ʽ������������ͼ�ε����ʣ���ס�����ľ��빫ʽ������������֮���߶���̽�����·�����⣻���÷������۵�˼�뷽�������3��С�⣮

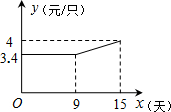 ��ԭʳƷ��˾�ӵ�һ��������������Ҫ����15������ɣ�Լ���������ӵij�����Ϊÿֻ5Ԫ��Ϊ��ʱ���������ҵ�������¹��ˣ����¹���С����x����������������Ϊnֻ��n��x�������¹�ϵʽ��$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}��0��x��5��\\��5��x��15��\end{array}$��
��ԭʳƷ��˾�ӵ�һ��������������Ҫ����15������ɣ�Լ���������ӵij�����Ϊÿֻ5Ԫ��Ϊ��ʱ���������ҵ�������¹��ˣ����¹���С����x����������������Ϊnֻ��n��x�������¹�ϵʽ��$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}��0��x��5��\\��5��x��15��\end{array}$�� ��ͼ����ƽ��ֱ������ϵ�У�����Rt��ABC��ֱ�Ƕ�����y���ϣ�б��BC��x���ϣ�AB=AC=4$\sqrt{2}$��DΪб��BC���е㣬��P�ɵ�A�������߶�AB�������˶���P���ǵ�P����AD�ĶԳƵ㣬P��P��y���ڵ�F����Q�ɵ�D����������DC�����������˶����������ı���QDPP����ƽ���ı��Σ���?QDPP������ΪS��DQ=x��
��ͼ����ƽ��ֱ������ϵ�У�����Rt��ABC��ֱ�Ƕ�����y���ϣ�б��BC��x���ϣ�AB=AC=4$\sqrt{2}$��DΪб��BC���е㣬��P�ɵ�A�������߶�AB�������˶���P���ǵ�P����AD�ĶԳƵ㣬P��P��y���ڵ�F����Q�ɵ�D����������DC�����������˶����������ı���QDPP����ƽ���ı��Σ���?QDPP������ΪS��DQ=x��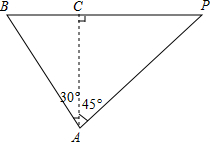 ��ͼ��һ���ִ�ԭ��A�������ı�ƫ��45��������һ����P���ִ����ű�ƫ��30������4Сʱ����B������ʱ����P�������ִ������������ϣ���֪�ִ����ٶ�Ϊ25����/ʱ�����ִ���B��ʱ�����P�ľ��루����������ţ���
��ͼ��һ���ִ�ԭ��A�������ı�ƫ��45��������һ����P���ִ����ű�ƫ��30������4Сʱ����B������ʱ����P�������ִ������������ϣ���֪�ִ����ٶ�Ϊ25����/ʱ�����ִ���B��ʱ�����P�ľ��루����������ţ���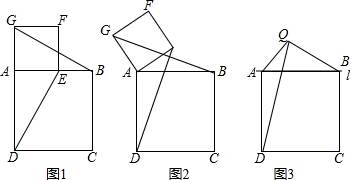
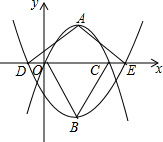 ��ͼ����ƽ��ֱ������ϵ�У�������y=a1��x-2��2+2��y=a2��x-2��2-3�Ķ���ֱ�ΪA��B����x��ֱ��ڵ�O��C��D��E������D������Ϊ��-1��0�������ADE���BOC�������Ϊ1��
��ͼ����ƽ��ֱ������ϵ�У�������y=a1��x-2��2+2��y=a2��x-2��2-3�Ķ���ֱ�ΪA��B����x��ֱ��ڵ�O��C��D��E������D������Ϊ��-1��0�������ADE���BOC�������Ϊ1��
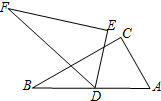 ������ȫ�غϵ�ֱ��������Rt��ABC��Rt��DEF��ֱ�DZ߷ֱ�Ϊ3cm��4cm����D������AB���е㣬��DEF�����Ƶ�Dת������Rt��DEF��ת��һ����AB��ֱʱ�����������ص��������Ϊ$\frac{75}{64}$��$\frac{69}{32}$��$\frac{25}{12}$��
������ȫ�غϵ�ֱ��������Rt��ABC��Rt��DEF��ֱ�DZ߷ֱ�Ϊ3cm��4cm����D������AB���е㣬��DEF�����Ƶ�Dת������Rt��DEF��ת��һ����AB��ֱʱ�����������ص��������Ϊ$\frac{75}{64}$��$\frac{69}{32}$��$\frac{25}{12}$��