题目内容
2.用a、b、c作三角形的三边,其中不能构成的直角三角形的是( )| A. | b2=(a+c)(a-c) | B. | a:b:c=1:2:$\sqrt{3}$ | C. | a=32,b=42,c=52 | D. | a=6,b=8,c=10 |
分析 根据选项中的数据,由勾股定理的逆定理可以判断a、b、c三边组成的三角形是否为直角三角形.勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
解答 解:A、∵b2=(a+c)(a-c),
∴b2=a2-c2,
∴b2+c2=a2,
∴能构成直角三角形,故选项A错误;
B、∵a:b:c=1:2:$\sqrt{3}$,
∴设a=x,则b=2x,c=$\sqrt{3}$x,
∵x2+($\sqrt{3}$x)2=(2x)2,
∴能构成直角三角形,故选项B错误;
C、∵a=32,b=42,c=52,
∴a2+b2=(32)2+(42)2=81+256=337≠(52)2,
∴不能构成直角三角形,故选项C正确;
D、∵a=6,b=8,c=10,
62+82=36+64=100=102,
∴能构成直角三角形,故选项D错误;
故选C.
点评 本题考查勾股定理的逆定理,利用勾股定理的逆定理时,可用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.

练习册系列答案
相关题目
12.某校八年级(1)班20名学生某次数学测验的成绩统计如表:
(1)若这20名学生成绩的平均数为82分,求x和y的值.
(2)在(1)的条件下,求这20名学生本次测验成绩的众数和中位数.
| 成绩(分) | 60 | 70 | 80 | 90 | 100 |
| 人数(人) | 1 | 5 | x | y | 2 |
(2)在(1)的条件下,求这20名学生本次测验成绩的众数和中位数.
 如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).
如图,菱形ABCD在平面直角坐标系中,点A位坐标原点,点B在x轴正半轴上,若点D的坐标为(1,$\sqrt{3}$),则点C的坐标为(3,$\sqrt{3}$).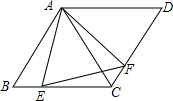 如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合.
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合. 如图,已知抛物线y=ax2-5ax+4经过△ABC的三个顶点,BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,已知抛物线y=ax2-5ax+4经过△ABC的三个顶点,BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.