题目内容
17.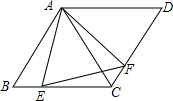 如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合.
如图,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为等边三角形,点E,F分别在菱形的边BC,CD上滑动,且E,F不与B,C,D重合.(1)求证:BE=CF;
(2)当点E,F在BC,CD上滑动时,四边形AECF的面积是否发生变化?如果不变,求出这个定值,如果变化,说明理由.
分析 (1)利用菱形的性质和等边三角形的性质,根据SAS证明△ABE≌△ACF,即可求得BE=CF;
(2)根据△ABE≌△ACF可得S△ABE=S△ACF,根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC得出四边形AECF的面积不会发生变化;再作AH⊥BC于点H.求出AH的值,根据S四边形AECF=S△ABC=$\frac{1}{2}$BC•AH,代入计算即可求解.
解答 (1)证明:∵在菱形ABCD中,∠BAD=120°,
∴∠B=60°,∠BAC=$\frac{1}{2}$∠BAD=60°,
∴△ABC为等边三角形,
∴AB=BC=AC.
∵△AEF为等边三角形,
∴AE=AF,∠EAF=60°,
∴∠BAC-∠EAC=∠EAF-∠EAC,
即∠BAE=∠CAF,
∴△BAE≌△CAF,
∴BE=CF; (2)解:四边形AECF的面积不会发生变化.理由如下:
(2)解:四边形AECF的面积不会发生变化.理由如下:
∵△BAE≌△CAF,
∴S△ABE=S△ACF,
∴S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,
∵△ABC的面积是定值,
∴四边形AECF的面积不会发生变化.
如图,作AH⊥BC于点H.
∵AB=AC=BC=4,
∴BH=$\frac{1}{2}$BC=2,
AH=AB•sin∠B=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴S四边形AECF=S△ABC=$\frac{1}{2}$BC•AH=$\frac{1}{2}$×4×2$\sqrt{3}$=4$\sqrt{3}$.
点评 本题考查了菱形的性质、全等三角形判定与性质及三角形面积的计算,求证△ABE≌△ACF是解题的关键,难度适中.

练习册系列答案
相关题目
8.下列从左到右的变形中,是分解因式的是( )
| A. | a2-4a+5=a(a-4)+5 | B. | (x+2)(x+3)=x2+5x+6 | C. | a2-9b2=(a+3b)(a-3b) | D. | x+1=x(1+$\frac{1}{x}$) |
5.[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-$\sqrt{2}$]的一次函数是正比例函数,则关于x的方程x+$\frac{1}{m}$=$\sqrt{2}$的解为( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
2.用a、b、c作三角形的三边,其中不能构成的直角三角形的是( )
| A. | b2=(a+c)(a-c) | B. | a:b:c=1:2:$\sqrt{3}$ | C. | a=32,b=42,c=52 | D. | a=6,b=8,c=10 |
9.如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是( )
| A. | 10 | B. | 11 | C. | 16 | D. | 26 |
 如图已知BE、EC分别平分∠ABC、∠BCD,且∠1与∠2互余,试说明AB∥DC.
如图已知BE、EC分别平分∠ABC、∠BCD,且∠1与∠2互余,试说明AB∥DC.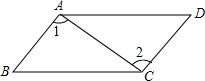 如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠BAD=∠BCD,∠1=∠2,求证:四边形ABCD是平行四边形. 如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(3,0).点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=a(x-1)2+4与x轴交于A、B两点,与y轴交于点C,且点B的坐标为(3,0).点P在这条抛物线上,且不与B、C两点重合.过点P作y轴的垂线与射线BC交于点Q以PQ为边作Rt△PQF,使∠PQF=90°,点F在点Q的下方,且QF=1.设点P的横坐标为m.