题目内容
10.计算:($\sqrt{32}$+3$\sqrt{6}$)÷2$\sqrt{2}$-3$\sqrt{(-\frac{2}{3})^{2}}$.分析 首先进行二次根式的化简,然后进行同类二次根式的合并.
解答 解:原式=(4$\sqrt{2}$+3$\sqrt{6}$)÷2$\sqrt{2}$-3×$\frac{2}{3}$
=2+$\frac{3}{2}$$\sqrt{3}$-2
=$\frac{3}{2}\sqrt{3}$.
点评 本题考查了二次根式的混合运算,解答本题的关键是掌握二次根式的化简及同类二次根式的合并.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.为了解某市八年级学生的课外数学阅读的时间,从中随机调查了400名学生的课外数学阅读的时间.下列说法正确的是( )
| A. | 某市八年级学生是总体 | |
| B. | 每一名八年级学生是个体 | |
| C. | 400名八年级学生是总体的一个样本 | |
| D. | 样本容量是400 |
5.[a,b]为一次函数y=ax+b(a≠0,a,b为实数)的“关联数”.若“关联数”[1,m-$\sqrt{2}$]的一次函数是正比例函数,则关于x的方程x+$\frac{1}{m}$=$\sqrt{2}$的解为( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
2.用a、b、c作三角形的三边,其中不能构成的直角三角形的是( )
| A. | b2=(a+c)(a-c) | B. | a:b:c=1:2:$\sqrt{3}$ | C. | a=32,b=42,c=52 | D. | a=6,b=8,c=10 |
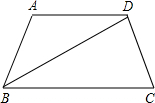 如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC.
如图,在四边形ABCD中,AD∥BC,BD平分∠ABC,∠A=2∠ABC,∠C=∠ABC. 已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答:
已知一次函数与反比例函数的图象交于点P(-2,1)和Q(1,m),如图是在同一直角坐标系中这两个函数图象的示意图,观察图象并回答: 如图,在?ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连结CQ.
如图,在?ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连结CQ.