题目内容
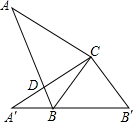 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是考点:旋转的性质
专题:
分析:根据三角形的内角和定理列式求出∠B,再由旋转的性质可得BC=B′C,∠A′=∠A,∠B′=∠B,然后利用等边对等角可得∠B′BC=∠B′,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:∵∠C=90°,∠A=35°,
∴∠B=90°-35°=55°,
∵△ABC旋转到△A′B′C 的位置,
∴BC=B′C,∠A′=∠A=35°,∠B′=∠B=55°,
∴∠B′BC=∠B′=55°,
∴∠A′CB=∠B′BC-∠A′=55°-35°=20°.
故答案为:20°.
∴∠B=90°-35°=55°,
∵△ABC旋转到△A′B′C 的位置,
∴BC=B′C,∠A′=∠A=35°,∠B′=∠B=55°,
∴∠B′BC=∠B′=55°,
∴∠A′CB=∠B′BC-∠A′=55°-35°=20°.
故答案为:20°.
点评:本题考查了旋转的性质,等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记各性质是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
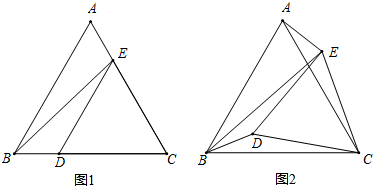 已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.
已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.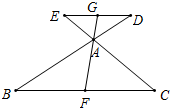 如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.
如图,已知△ABC中,DE∥BC,分别交于BA、CA的延长线于D、E,F为BC中点,FA的延长线交DE于点G,求证:DG=EG.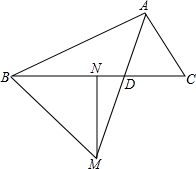 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.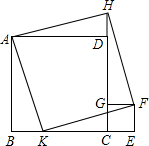 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.