题目内容
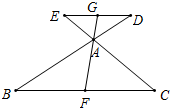如图，已知△ABC中，DE∥BC，分别交于BA、CA的延长线于D、E，F为BC中点，FA的延长线交DE于点G，求证：DG=EG．考点：相似三角形的判定与性质
专题：证明题
分析：首先利用平行线的性质来判断△DAG∽△BAF，得到关于线段DG的比例式；运用同样的方法得到关于线段EG的比例式，借助中点的定义即可解决问题．
解答：证明：∵DE∥BC，
∴△DAG∽△BAF，
∴
=
；
同理可证：
=
；
∴
=
；
又∵F为BC的中点，
∴BF=CF，
∴DG=EG．
证明：∵DE∥BC，∴△DAG∽△BAF，
∴
| DG |
| BF |
| GA |
| AF |
同理可证：
| EG |
| CF |
| GA |
| AF |
∴
| DG |
| BF |
| EG |
| CF |
又∵F为BC的中点，
∴BF=CF，
∴DG=EG．
点评：考查了相似三角形的判定及其性质问题；解题的关键是准确列出比例式，灵活变形．
练习册系列答案
相关题目
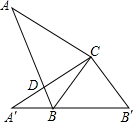如图，在直角△ABC中，∠C=90°，∠A=35°，以直角顶点C为旋转中心，将△ABC旋转到△A′B′C 的位置，其中A、B′分别是A、B的对应点，且点B在斜边A′B′上，则∠A′CB的度数是
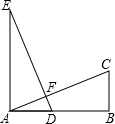已知，如图：AE⊥AB，BC⊥AB，AE=AB，ED=AC．求证：ED⊥AC．
如图，△ACO为等腰直角三角形，AC=CO，M为AO的中点，CN⊥y轴于N，求∠MNO的度数．