题目内容
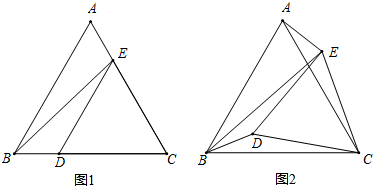 已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.
已知△ABC和△EDC都是等边三角形,将∠CDE绕C点旋转.(1)如图1,当边CD、CE分别在BC、AC上时,求证:∠AEB=∠EBD+60°;
(2)如图2,当CD在BC的上方时,猜想∠AEB和∠EBD的度数的数量关系,并给予证明.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:(1)根据三角形内角与外角的性质可直接得到∠C+∠EBC=∠AEB;
(2)首先证明△BDC≌△AEC可得∠1=∠2,再根据三角形内角与外角的性质可得∠1+∠AEB=∠EBD+∠2+∠ACB,进而可得∠AEB=∠EBD+60°.
(2)首先证明△BDC≌△AEC可得∠1=∠2,再根据三角形内角与外角的性质可得∠1+∠AEB=∠EBD+∠2+∠ACB,进而可得∠AEB=∠EBD+60°.
解答:(1)证明:∵△ABC是等边三角形,
∴∠C=60°,
∵边CD、CE分别在BC、AC上,
∴∠C+∠EBC=∠AEB,
∴∠AEB=∠EBD+60°;
(2)解:∠AEB=∠EBD+∠ACB=∠EBD+60°;
理由:∵△ABC和△EDC都是等边三角形,
∴EC=DC,AC=CB,∠ECD=∠ACB=60°,
∴∠ACE=∠BCD,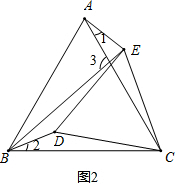
在△BDC和△AEC中
,
∴△BDC≌△AEC(SAS),
∴∠1=∠2,
∵∠1+∠AEB=∠3,∠EBD+∠2+∠ACB=∠3,
∴∠1+∠AEB=∠EBD+∠2+∠ACB,
∴∠AEB=∠EBD+∠ACB=∠EBD+60°.
∴∠C=60°,
∵边CD、CE分别在BC、AC上,
∴∠C+∠EBC=∠AEB,
∴∠AEB=∠EBD+60°;
(2)解:∠AEB=∠EBD+∠ACB=∠EBD+60°;
理由:∵△ABC和△EDC都是等边三角形,
∴EC=DC,AC=CB,∠ECD=∠ACB=60°,
∴∠ACE=∠BCD,

在△BDC和△AEC中
|
∴△BDC≌△AEC(SAS),
∴∠1=∠2,
∵∠1+∠AEB=∠3,∠EBD+∠2+∠ACB=∠3,
∴∠1+∠AEB=∠EBD+∠2+∠ACB,
∴∠AEB=∠EBD+∠ACB=∠EBD+60°.
点评:本题考查了全等三角形的性质和判定,以及三角形内角与外角的性质,关键是掌握①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
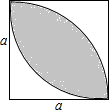 一块正方形苗圃的造型如图所示(单位:m),它的阴影部分和空白部分将分成两种颜色的花地.根据所给的数据,求图中阴影部分的面积和空白部分的面积各是多少?
一块正方形苗圃的造型如图所示(单位:m),它的阴影部分和空白部分将分成两种颜色的花地.根据所给的数据,求图中阴影部分的面积和空白部分的面积各是多少?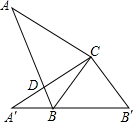 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是 如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )
如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )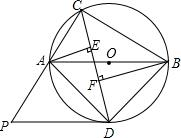 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明. 如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证:
如图所示,在⊙O中,AB是直径,BD是弦,半径OC∥BD,求证: