题目内容
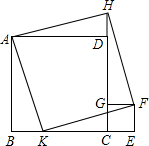 已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.考点:正方形的判定与性质
专题:证明题
分析:根据正方形的性质得出AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,求出∠ADH=∠HGF=∠E=∠B=90°,BK=GF=DH=EF,KE=GH=AB=AD,证△ABK≌△KEF≌△HGF≌△ADH,根据全等三角形的性质推出AK=KF=HF=AH,∠BAK=HAD,求出∠HAK=∠BAD=90°,根据正方形的判定得出即可.
解答:证明:∵四边形ABCD和四边形CEFG是正方形,
∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,
∴∠ADH=∠HGF=∠E=∠B=90°,
∵DH=CE,BK=CE,
∴BK=GF=DH=EF,KE=GH=AB=AD,
在△ABK、△KEF、△HGF、△ADH中
∴△ABK≌△KEF≌△HGF≌△ADH,
∴AK=KF=HF=AH,∠BAK=HAD,
∵∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,
∴四边形AKFH为正方形.
∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,
∴∠ADH=∠HGF=∠E=∠B=90°,
∵DH=CE,BK=CE,
∴BK=GF=DH=EF,KE=GH=AB=AD,
在△ABK、△KEF、△HGF、△ADH中
|
∴△ABK≌△KEF≌△HGF≌△ADH,
∴AK=KF=HF=AH,∠BAK=HAD,
∵∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,
∴四边形AKFH为正方形.
点评:本题考查了正方形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是推出△ABK≌△KEF≌△HGF≌△ADH,注意:有一个角是直角的菱形是正方形.

练习册系列答案
相关题目
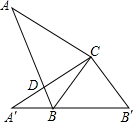 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是 如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.
如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.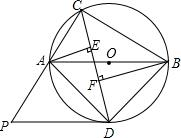 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明. 如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE.
如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE.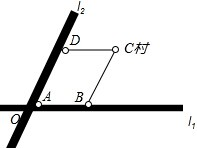 如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是
如图所示,两条笔直的公路l1、l2相交于点O,村庄C的村民在公路的旁边建三个加工厂A、B、D,已知AD=AB=6km,CD=CB=5km,村庄C到公路l1的距离为4km,则村庄C到公路l2的距离是