题目内容
直线y=
x+4与x轴交于点B,与y轴交于点A,直线y=-2x+b过点A且与x轴交于点C.求:
(1)A、B、C三点的坐标;
(2)△ABC的面积.
| 4 |
| 3 |
(1)A、B、C三点的坐标;
(2)△ABC的面积.
考点:一次函数图象上点的坐标特征
专题:计算题
分析:(1)先利用坐标轴上点的坐标特征可确定B(-3,0),A(0,4),再把A点坐标代入y=-2x+b求出b的值,确定此函数解析式,然后再求C点坐标;
(2)根据三角形面积公式求解.
(2)根据三角形面积公式求解.
解答:解 :(1)当y=0时,
:(1)当y=0时,
x+4=0,解得x=-3,则B点坐标为(-3,0);
当x=0时,y=
x+4=4,则A点坐标为(0,4),
∵直线y=-2x+b过点A(0,4),
∴b=4,
∵当y=0时,y=-2x+4=0,解得x=2,
∴C点坐标为(2,0);
(2)△ABC的面积=
×4×(2+3)=10.
 :(1)当y=0时,
:(1)当y=0时,| 4 |
| 3 |
当x=0时,y=
| 4 |
| 3 |
∵直线y=-2x+b过点A(0,4),
∴b=4,
∵当y=0时,y=-2x+4=0,解得x=2,
∴C点坐标为(2,0);
(2)△ABC的面积=
| 1 |
| 2 |
点评:本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-bk,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下面的说法不正确的是( )
| A、解方程指的是求方程的解的过程 |
| B、解方程指的是方程变形的过程 |
| C、解方程指的是求方程中未知数的值,使方程两边相等的过程 |
| D、解方程指的是使方程中未知数变为已知数的过程 |
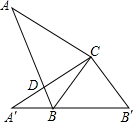 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是