题目内容
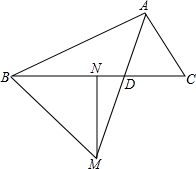 如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.
如图,MN是BC边上的垂直平分线,射线AD交MN于点M,交BC于点D,连接BM.若∠BAM=∠CAM,求证:∠BAM+∠BMN=90°.考点:全等三角形的判定与性质,线段垂直平分线的性质
专题:证明题
分析:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,由ME⊥AB,MF⊥AC,所以∠3=∠4=90°,由四边形的内角和为360°,可得∠BAC+∠EMF=180°,由∠1=∠2,且ME⊥AB,MF⊥AC,可得ME=MF,由MN是BC边上的垂直平分线,可得BM=MC,进而得到Rt△BME≌Rt△CMF(HL),所以∠5=∠6,所以∠5+∠EMC=∠6+∠EMC,即:∠EMF=∠BMC,由MN是BC边上的垂直平分线,所以BM=CM,所以∠BMN=∠CMN=
∠BMC,所以∠BAM+∠BMN=
∠BAC+
∠BMC=
(∠BAC+∠BMC)=
×180°=90°.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: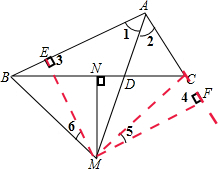 证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,
证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,
∵ME⊥AB,MF⊥AC,
∴∠3=∠4=90°,
∵四边形的内角和为360°,
即∠3+∠4+∠BAC+∠EMF=360°,
∴∠BAC+∠EMF=180°,
∵∠BAM=∠CAM,即∠1=∠2,
且ME⊥AB,MF⊥AC,
∴ME=MF,
∵MN是BC边上的垂直平分线,
∴BM=MC,
在Rt△BME和Rt△CMF中,
,
∴Rt△BME≌Rt△CMF(HL),
∴∠5=∠6,
∴∠5+∠EMC=∠6+∠EMC,
即:∠EMF=∠BMC,
∵∠BAC+∠EMF=180°,
∴∠BAC+∠BMC=180°,
∵∠BAM=∠CAM,
∴∠BAM=
∠BAC,
∵MN是BC边上的垂直平分线,
∴BM=CM,
∴∠BMN=∠CMN=
∠BMC,
∴∠BAM+∠BMN=
∠BAC+
∠BMC=
(∠BAC+∠BMC)=
×180°=90°.
 证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,
证明:过点M作ME⊥AB,垂足为E,MF⊥AC,垂足为F,连接MC,∵ME⊥AB,MF⊥AC,
∴∠3=∠4=90°,
∵四边形的内角和为360°,
即∠3+∠4+∠BAC+∠EMF=360°,
∴∠BAC+∠EMF=180°,
∵∠BAM=∠CAM,即∠1=∠2,
且ME⊥AB,MF⊥AC,
∴ME=MF,
∵MN是BC边上的垂直平分线,
∴BM=MC,
在Rt△BME和Rt△CMF中,
|
∴Rt△BME≌Rt△CMF(HL),
∴∠5=∠6,
∴∠5+∠EMC=∠6+∠EMC,
即:∠EMF=∠BMC,
∵∠BAC+∠EMF=180°,
∴∠BAC+∠BMC=180°,
∵∠BAM=∠CAM,
∴∠BAM=
| 1 |
| 2 |
∵MN是BC边上的垂直平分线,
∴BM=CM,
∴∠BMN=∠CMN=
| 1 |
| 2 |
∴∠BAM+∠BMN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了全等三角形的判定与性质,解题的关键是:正确添加辅助线.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
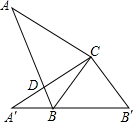 如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是
如图,在直角△ABC中,∠C=90°,∠A=35°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C 的位置,其中A、B′分别是A、B的对应点,且点B在斜边A′B′上,则∠A′CB的度数是 如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( )
如图,在Rt△ABCk,∠BAC=90°,∠ABC=65°,△AB1C1由△ABC绕点A顺时针旋转90°得到的(点B1与点B是对应点,点C1与点C是对应点),边接CC1,则∠CC1B1的度数是( ) 如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.
如图,△ACO为等腰直角三角形,AC=CO,M为AO的中点,CN⊥y轴于N,求∠MNO的度数.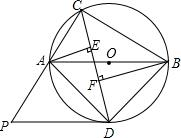 如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明.
如图,△ABC内接于⊙O,且AB为⊙O的直径,∠ACB的平分线交⊙O于点D,过点D作⊙O的切线PD交CA的延长线于点P,过点A作AE⊥CD于点E,过点B作BF⊥CD于点F.试猜想线段AE、EF、BF之间的关系,并加以证明. 如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE.
如图,CA、CD分别与⊙O相切于A、D,AB为⊙O的直径,CO的延长线交⊙O于E,求证:∠B=2∠BDE.