题目内容
12.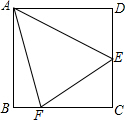 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
分析 如图,作辅助线,首先证明△AFE≌△AGE,进而得到EF=FG,问题即可解决.
解答 证明:∵四边形ABCD是正方形,
∴AB=AD,
∴把△ABF绕点A逆时针旋转90°至△ADG,可使AB与AD重合,如图: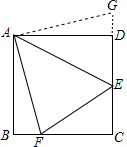
∴∠BAF=∠DAG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAF+∠DAE=45°,
∴∠EAF=∠EAG,
∵∠ADG=∠ADC=∠B=90°,
∴∠EDG=180°,点E、D、G共线,
在△AFE和△AGE中,
$\left\{\begin{array}{l}{AG=AF}\\{∠FAE=∠EAG}\\{AE=AE}\end{array}\right.$,
∴△AFE≌△AGE(SAS),
∴EF=EG,
即:EF=BE+DF,
∵E为CD的中点,边长为$6\sqrt{2}$的正方形ABCD,
∴CD=BC=6$\sqrt{2}$,DE=CE=3$\sqrt{2}$,∠C=90°,
∴设BF=x,则CF=6$\sqrt{2}$-x,EF=3$\sqrt{2}$+x,
在Rt△CFE中,由勾股定理得:EF2=CE2+CF2,
(3$\sqrt{2}$+x)2=(3$\sqrt{2}$)2+(6$\sqrt{2}$-x)2,
解得:x=2$\sqrt{2}$,
即BF=2$\sqrt{2}$,
故选A.
点评 本题考查了正方形的性质、全等三角形的判定及其性质的应用,解题的关键是作辅助线,构造全等三角形.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20. 如图,矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为( )
如图,矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为( )
 如图,矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为( )
如图,矩形ABCD中,AC与BD交于点O,若∠AOB=60°,AB=5,则对角线AC的长为( )| A. | 5 | B. | 7.5 | C. | 10 | D. | 15 |
7. 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )
 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
17. 如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )
如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )
 如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )
如图,E、F、G、H分别是四边形ABCD四条边的中点,则四边形EFGH一定是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
2.下列计算正确的是( )
| A. | 3$\sqrt{2}$-$\sqrt{2}$=3 | B. | $\sqrt{2}$+$\sqrt{5}$=$\sqrt{7}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{(-15)^{2}}$=-15 |
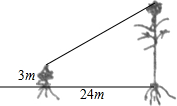 有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解)
有一只喜鹊在一棵3m高的小树上觅食,它的巢筑在距离该树24m远的一棵大树上,大树高14m,且巢离树顶部1m,当它听到巢中幼鸟的叫声,立即赶过去,如果它飞行的速度为5m/s,那它至少需要多少时间才能赶回巢中?(画出符合题意的几何图形,并求解) 如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )
如图,在△ABC中,BD平分∠ABC,ED∥BC,已知AB=3,AD=1,则△AED的周长为( )