题目内容
7. 如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )
如图,已知AB=A1B,A1B1=A1A2,A2B2=A2A3,A3B3=A3A4…,若∠A=70°,则∠An-1AnBn-1的度数为( )| A. | $\frac{70}{{2}^{n}}$ | B. | $\frac{70}{{2}^{n+1}}$ | C. | $\frac{70}{{2}^{n-1}}$ | D. | $\frac{70}{{2}^{n+2}}$ |
分析 根据三角形外角的性质及等腰三角形的性质分别求出∠B1A2A1,∠B2A3A2及∠B3A4A3的度数,找出规律即可得出∠An-1AnBn-1的度数.
解答 解:∵在△ABA1中,∠A=70°,AB=A1B,
∴∠BA1A=70°,
∵A1A2=A1B1,∠BA1A是△A1A2B1的外角,
∴∠B1A2A1=$\frac{∠B{A}_{1}A}{2}$=35°;
同理可得,
∠B2A3A2=17.5°,∠B3A4A3=$\frac{1}{2}$×17.5°=$\frac{35°}{4}$,
∴∠An-1AnBn-1=$\frac{70°}{{2}^{n-1}}$.
故选:C.
点评 本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠B1C2A1,∠B2A3A2及∠B3A4A3的度数,找出规律是解答此题的关键.

练习册系列答案
相关题目
15. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:
(1)AE=BF;(2)AE⊥BF;(3)AD=OE;(4)S△AOB=S四边形DEOF.
其中正确的有( )
 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:
如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE与BF相交于O;下列结论:(1)AE=BF;(2)AE⊥BF;(3)AD=OE;(4)S△AOB=S四边形DEOF.
其中正确的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2. 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
 把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )
把边长相等的正五边形ABCDE和正方形ABFG按照如图所示的方式叠合在一起,则∠EAG的度数是( )| A. | 18° | B. | 20° | C. | 28° | D. | 30° |
12.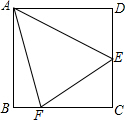 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
19.下列说法正确的是( )
| A. | 三角形可以分为等边三角形、直角三角形、钝角三角形 | |
| B. | 如果一个三角形的一个外角大于与它相邻的内角,则这个三角形为锐角三角形 | |
| C. | 各边都相等的多边形是正多边形 | |
| D. | 五边形有五条对角线 |
16. 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )| A. | $\sqrt{10}$ | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 不确定 |
 将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.
将∠B,∠E按如图所示的方式放置.请你从下列三项:①∠B=∠E;②AB∥DE;③BC∥EF中选择两项作为条件,填入“已知”栏中,另一项作为结论,填入“求证”栏中,并证明.


