题目内容
17．
如图，E、F、G、H分别是四边形ABCD四条边的中点，则四边形EFGH一定是（ ）| A． | 平行四边形 | B． | 矩形 | C． | 菱形 | D． | 正方形 |
分析 顺次连接任意四边形四边中点所得的四边形，一组对边平行并且等于原来四边形某一对角线的一半，说明新四边形的对边平行且相等．所以是平行四边形．
解答 
解：如图，连接AC，
∵E、F、G、H分别是四边形ABCD边的中点，
∴HG∥AC，HG=$\frac{1}{2}$AC，EF∥AC，EF=$\frac{1}{2}$AC；
∴EF=HG且EF∥HG；
∴四边形EFGH是平行四边形．
故选：A．
点评 此题主要考查了平行四边形的判定以及三角形的中位线定理，根据已知利用三角形中位线定理得出EH∥BD，EH=$\frac{1}{2}$BD，FG∥BD，FG=$\frac{1}{2}$BD是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，点E是等边△ABC外一点，点D是BC边上一点，AD=BE，∠CAD=∠CBE，连结ED，EC．
8．
在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上．已知正方形A1B1C1D1的边长为1，∠C1B1O=30°，B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是（ ）
在平面直角坐标系中，正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置，其中点B1在y轴上，点C1、E1、E2、C2、E3、E4、C3…在x轴上．已知正方形A1B1C1D1的边长为1，∠C1B1O=30°，B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是（ ）| A． | ${（\frac{1}{2}）}^{2015}$ | B． | ${（\frac{1}{2}）}^{2016}$ | C． | ${（\frac{\sqrt{3}}{3}）}^{2015}$ | D． | ${（\frac{\sqrt{3}}{3}）}^{2016}$ |
5．下列各数中，介于正整数6和7之间的数是（ ）
| A． | $\sqrt{41}$ | B． | $\sqrt{52}$ | C． | $\sqrt{26}$ | D． | $\root{3}{38}$ |
12．
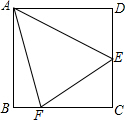如图，在边长为$6\sqrt{2}$的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF=45°，连接EF，则BF的长为（ ）
如图，在边长为$6\sqrt{2}$的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF=45°，连接EF，则BF的长为（ ）| A． | $2\sqrt{2}$ | B． | 3 | C． | $3\sqrt{2}$ | D． | 4 |
如图，已知菱形ABCD中，AC，BD相交于点O，点E是AB的中点，OE=5cm，则菱形的周长是40cm．
已知：P是正方形ABCD对角线AC上一点，PE⊥AB，PF⊥BC，E、F分别为垂足．
如图，在矩形ABCD中，AD=2AB，E是AD上一点，且BE=BC，则∠ECD的度数是15°．