题目内容
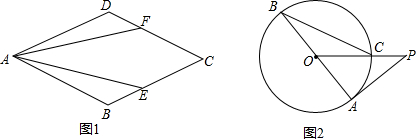
1.如图,在△ABC中,∠BAC的平分线交BC于点D.(1)如图1,若∠B=62°,∠C=38°,AE⊥BC于点E,求∠EAD的度数;
(2)如图2,若点F是AD延长线上的一点,∠BAF、∠BDF的平分线交于点G,∠B=x°,∠C=y°(x>y),求∠G的度数.

分析 (1)先根据三角形内角和定理求出∠BAC的度数,再由角平分线的性质求出∠BAD的度数,由直角三角形的性质求出∠BAE的度数,根据∠EAD=∠BAD-∠BAE即可得出结论;
(2)首先利用三角形内角和定理可求出∠BAC的度数,进而可求出∠BAD的度数,由题意可知∠BAG=$\frac{1}{4}$∠BAC,再利用已知条件和三角形外角和定理即可求出∠G的度数.
解答 解:(1)∵在△ABC中,∠B=62°,∠C=38°,
∴∠BAC=180°-62°-38°=80°.
∵∠BAC的平分线交BC于点D,
∴∠BAD=$\frac{1}{2}$∠BAC=40°.
∵AE⊥BC于点E,
∴∠AEB=90°,
∴∠BAE=90°-62°=28°,
∴∠EAD=∠BAD-∠BAE=40°-28°=12°;
(2)∵∠B=x°,∠C=y°,
∴∠BAC=180°-x°-y°,
∵∠BAC的平分线交BC于点D,
∴∠BAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$(180°-x°-y°),AG平分∠BAD,
∴∠BAG=$\frac{1}{2}$∠BAD=$\frac{1}{4}$(180°-x°-y°),
∵∠BDF=∠BAD+∠B,
∴∠G=$\frac{1}{2}$∠BDF-∠GAD=$\frac{1}{2}$x°,
点评 本题考查角平分线的定义、三角形外角的性质及三角形的内角和定理.求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
11.因式分解的结果是(x+y-z)(x-y+z)的多项式是( )
| A. | x2-(y+z)2 | B. | (x-y)2-z2 | C. | -(x-y)2+z2 | D. | x2-(y-z)2 |
12.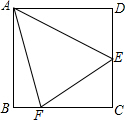 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
 如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )
如图,在边长为$6\sqrt{2}$的正方形ABCD中,E是边CD的中点,F在BC边上,且∠EAF=45°,连接EF,则BF的长为( )| A. | $2\sqrt{2}$ | B. | 3 | C. | $3\sqrt{2}$ | D. | 4 |
16. 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
 如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )
如图,矩形ABCD中,AB=4,BC=6,P是CD边上的中点,E是BC边上的一动点,M,N分别是AE、PE的中点,则随着点E的运动,线段MN长为( )| A. | $\sqrt{10}$ | B. | 4$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | 不确定 |
 已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.