题目内容
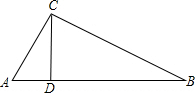已知Rt△ABC中，∠ACB=90°，CD⊥AB于点D，求证：| AC2 |
| BC2 |
| AD |
| BD |
考点：相似三角形的判定与性质
专题：证明题
分析：由条件可证得Rt△ACD∽Rt△ABC，可得
=
，所以有AC2=AB•AD①，同理可证得Rt△BCD∽Rt△BAC，可得
=
，所以有BC2=AB•BD②两式相除可得结论．
| AC |
| AB |
| AD |
| AC |
| BC |
| AB |
| BD |
| BC |
解答：证明：∵∠ACB=90°，CD⊥AB，
∴∠ADC=∠ACB=90°，且∠A=∠A，
∴Rt△ACD∽Rt△ABC，
∴
=
，
∴AC2=AB•AD ①，
同理可证得Rt△BCD∽Rt△BAC，可得
=
，
∴BC2=AB•BD ②
①÷②可得：
=
=
．
∴∠ADC=∠ACB=90°，且∠A=∠A，
∴Rt△ACD∽Rt△ABC，
∴
| AC |
| AB |
| AD |
| AC |
∴AC2=AB•AD ①，
同理可证得Rt△BCD∽Rt△BAC，可得
| BC |
| AB |
| BD |
| BC |
∴BC2=AB•BD ②
①÷②可得：
| AC2 |
| BC2 |
| AB•AD |
| AB•BD |
| AD |
| BD |
点评：本题主要考查三角形相似的判定和性质，解题的关键是把AC2、BC2化为线段的积．
练习册系列答案
相关题目
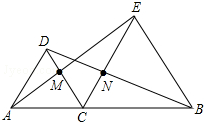如图，△DAC和△EBC均是等边三角形，AB、BC分别与CD、CE交于点M、N，有如下结论：
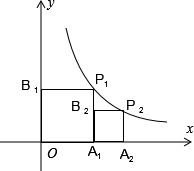如图，正方形OA1P1B1和正方形A1A2P2B2的顶点P1，P2都在函数y=