题目内容
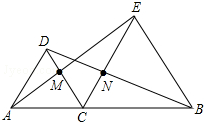 如图,△DAC和△EBC均是等边三角形,AB、BC分别与CD、CE交于点M、N,有如下结论:
如图,△DAC和△EBC均是等边三角形,AB、BC分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②△ACM≌△DCN;③CM=CN.
正确结论的个数是( )
| A、3个 | B、2个 | C、1个 | D、0个 |
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)由△DAC和△EBC都是等边三角形,利用等边三角形的性质得到AC=CD,EC=BC,且∠ACD=∠ECB=60°,利用等式的性质得到夹角相等,利用SAS得到△ACE≌△DCB.
(2)根据全等三角形对应角相等可得∠CAE=∠CDB,再利用“角边角”证明ACM和△DCN全等,从而判断②正确;
(3)利用全等三角形的对应角相等得到∠AEC=∠DBC,利用平角的定义得到∠DCE=60°,即∠DCE=∠NCB,再由夹边EC=BC,利用ASA得到△EMC≌△BNC,利用全等三角形对应边相等得到CM=CN,即可得到结果.
(2)根据全等三角形对应角相等可得∠CAE=∠CDB,再利用“角边角”证明ACM和△DCN全等,从而判断②正确;
(3)利用全等三角形的对应角相等得到∠AEC=∠DBC,利用平角的定义得到∠DCE=60°,即∠DCE=∠NCB,再由夹边EC=BC,利用ASA得到△EMC≌△BNC,利用全等三角形对应边相等得到CM=CN,即可得到结果.
解答:解:①∵△DAC和△EBC均是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS)
②由△ACE≌△DCB,
∴∠CAE=∠CDB,
在△ACM和△DCN中,
,
∴△ACM≌△DCN(ASA).
③∵△ACM≌△DCN,
∴CM=CN.
故选:A.
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
即∠ACE=∠BCD,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(SAS)
②由△ACE≌△DCB,
∴∠CAE=∠CDB,
在△ACM和△DCN中,
|
∴△ACM≌△DCN(ASA).
③∵△ACM≌△DCN,
∴CM=CN.
故选:A.
点评:本题考查了等边三角形的性质,全等三角形的判定与性质,平行线的判定,综合性较强,但难度不是很大,准确识图找出全等三角形是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
下列说法中正确的是( )
| A、非负有理数就是正有理数 |
| B、零表示没有,不是自然数 |
| C、正整数和负整数统称为整数 |
| D、整数和分数统称为有理数 |
下列判断正确的是( )
| A、“打开电视机,正在播NBA篮球赛”是必然事件 | ||||
B、“掷一枚硬币正面朝上的概率是
| ||||
| C、一组数据2,3,4,5,5,6的众数和中位数都是5 | ||||
D、甲组数据的方差
|
下列各式是一元一次方程的是( )
| A、-3x-y=0 | ||
| B、2x=0 | ||
C、2+
| ||
| D、3x2+x=8 |
下列运算正确的是( )
| A、2x2y+3xy2=5x3y |
| B、(-x)3•(-x)2=-x5 |
| C、(-a3)2+(-a2)3=1 |
| D、2x3+x2=3x5 |
下列结论中正确是( )
| A、两个有理数的和一定大于其中任何一个加数 |
| B、零加上一个数仍得这个数 |
| C、两个有理数的差一定小于被减数 |
| D、零减去一个数仍得这个数 |

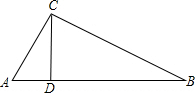 已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证:
已知Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求证: